Study Notes

Overview
Welcome to the definitive guide for Edexcel GCSE Chemistry Topic 3.8: Evaluating Experimental Data. This isn't just about number crunching; it's about developing a critical scientific mindset. In your exam, you'll be expected to scrutinize data, identify its limitations, and suggest concrete improvements. This skill is heavily tested, accounting for a significant portion of your AO3 (Analysis and Evaluation) marks, which make up 50% of your grade. You'll encounter these questions in various contexts, from titration experiments to reaction rate investigations. Mastering this topic means you can confidently tackle questions that ask you to assess the validity of results, ensuring you don't lose marks on common errors. This guide will equip you with the language and techniques examiners want to see.
Key Concepts
Concept 1: Accuracy, Precision, Repeatability, and Reproducibility
These four terms are the bedrock of data evaluation, and they are frequently confused. Let's clarify them.
- Accuracy: How close a measurement is to the true value. For example, if the true boiling point of a substance is 100°C and you measure it as 99.8°C, your result is highly accurate.
- Precision: How close repeated measurements are to each other. You could have three measurements of 98.1°C, 98.2°C, and 98.1°C. These are precise, but not accurate if the true value is 100°C. This indicates a systematic error.
- Repeatability: This is achieved when the same person repeats the experiment with the same method and equipment and gets similar, precise results. It's a measure of your own consistency.
- Reproducibility: This is achieved when a different person, or a different method/piece of equipment, yields similar results. It's the ultimate test of a method's validity.
Examiners award marks for using this terminology correctly. For instance, linking 'reproducibility' to a 'different operator' is a classic mark-scoring point.
Concept 2: Uncertainty and Errors
No measurement is perfect; all have a degree of uncertainty. Your job is to minimize it.
- Measurement Uncertainty: The potential variation in a measurement, often expressed as a range (e.g., ±0.05 cm³). This is determined by the resolution of the measuring instrument.
- Systematic Error: A consistent error that affects all measurements in the same way, often due to faulty equipment or a flawed method. For example, a thermometer that always reads 2°C too high. On a graph, a systematic error is often revealed when the line of best fit does not pass through the origin when it is expected to.
- Random Error: Unpredictable variations in measurements, such as parallax error when reading a scale or fluctuations in room temperature. These can be minimized by taking multiple readings and calculating a mean.
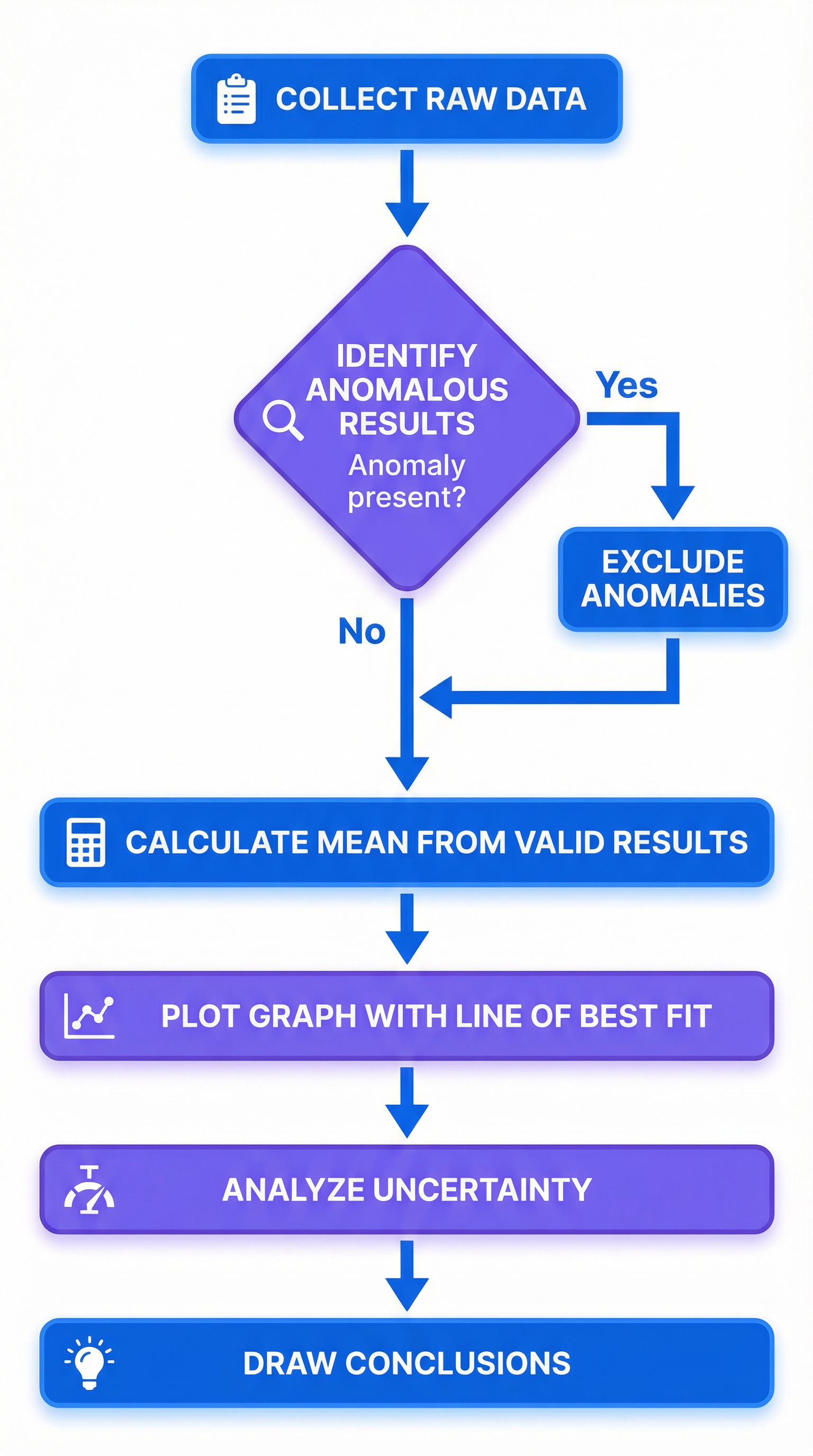
Concept 3: Anomalous Results and Mean Calculation
An anomalous result (or outlier) is a reading that does not fit the expected pattern. It is crucial that you can identify and handle these correctly.
Identifying Anomalies:
- In a table of repeat readings, it's the value that is significantly different from the others.
- On a graph, it's the point that lies far from the line of best fit.
Handling Anomalies:
- Identify the anomaly clearly. In an exam, you should circle it on the graph.
- Exclude it from any calculations. NEVER include an anomalous result when calculating the mean.
- Calculate the mean using only the concordant (close together) results. Credit is specifically awarded for this.
Example:
A student takes the following readings: 25.1 cm³, 25.3 cm³, 28.9 cm³, 25.2 cm³.
- The anomalous result is 28.9 cm³.
- The mean should be calculated as: (25.1 + 25.3 + 25.2) / 3 = 25.2 cm³.
Mathematical/Scientific Relationships
Calculating Percentage Uncertainty
This is a higher-tier skill but essential for top marks. It shows how significant the uncertainty is relative to the measurement itself.
Formula: Percentage Uncertainty = (Uncertainty / Measurement) x 100
- Uncertainty: The resolution of the instrument (e.g., for a burette, you have two readings, so the uncertainty is 2 x 0.05 cm³ = 0.1 cm³).
- Measurement: The value you recorded.
Example:
If you measure a titre of 25.00 cm³ with a burette (uncertainty ±0.05 cm³ per reading), the total uncertainty is 0.1 cm³.
Percentage Uncertainty = (0.1 / 25.00) x 100 = 0.4%
Practical Applications
This topic is directly tested through Required Practicals. For example, in a titration (a required practical), you might be asked to evaluate the results.
Improving the Experiment:
When asked to improve an experiment, be specific. 'Do it more carefully' or 'avoid human error' will score zero marks. Instead, suggest using apparatus with a higher resolution.
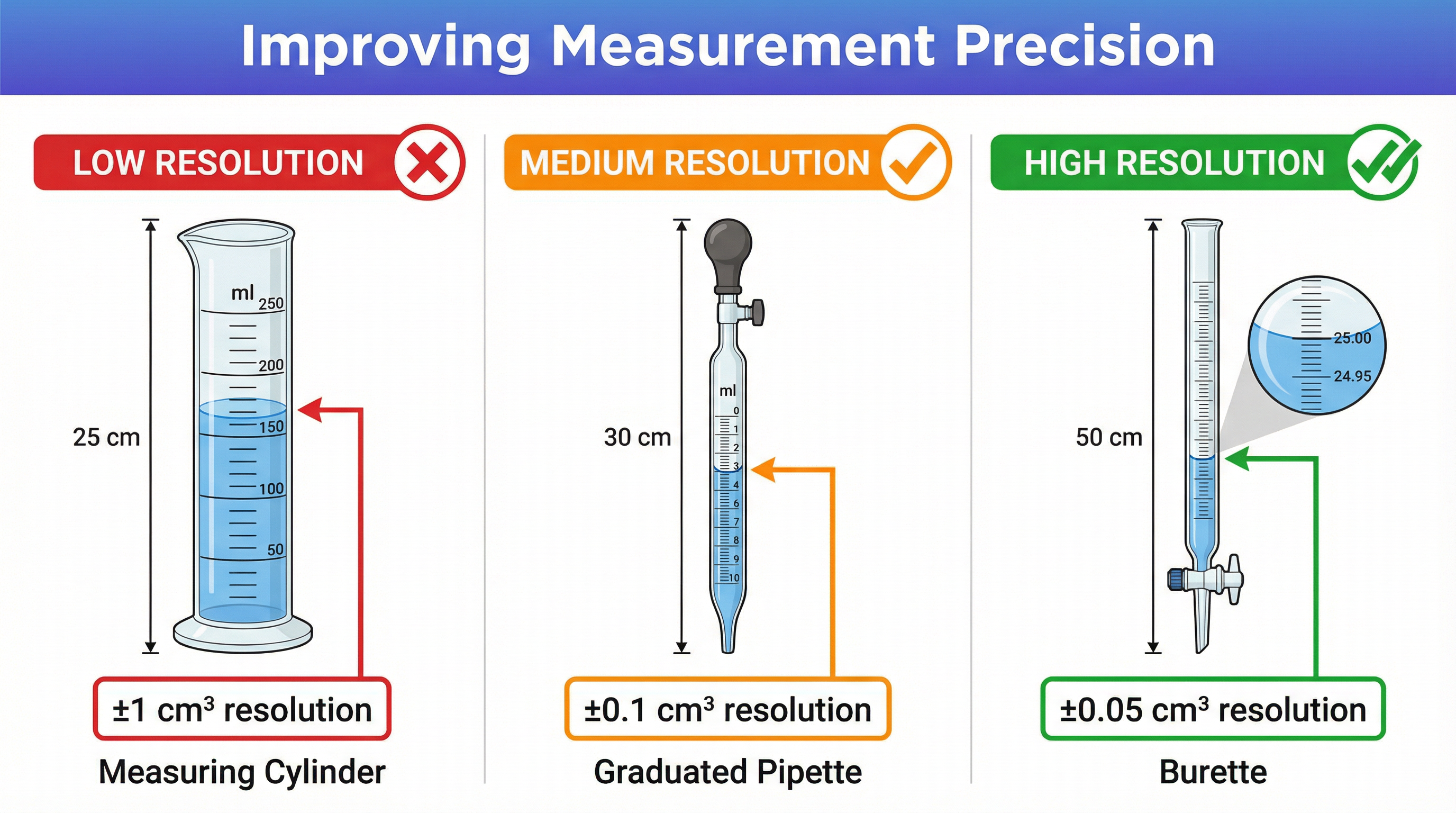
| Instead of... | Use... | Because... |
|---|---|---|
| Measuring Cylinder (±1 cm³) | Burette (±0.05 cm³ per reading) | It has a higher resolution, reducing measurement uncertainty. |
| Thermometer (±1 °C) | Digital Thermometer (±0.1 °C) | It provides more precise temperature readings. |
| Inverting a cylinder over water to collect gas | Gas Syringe (±1 cm³) | It more accurately measures the volume of gas produced. |
