Study Notes
Overview
Error intervals are a fundamental concept in mathematics that address the inherent uncertainty in all measurements. In your AQA GCSE exam, this topic (specification reference 1.7) is a test of precision and your ability to communicate the limits of accuracy using formal inequality notation. When a value is rounded or truncated, its true value lies within a specific range, and expressing this range correctly is key to earning marks. For Foundation candidates, the focus is on correctly identifying the lower and upper bounds for numbers rounded to a given degree of accuracy (e.g., decimal places, significant figures). For Higher tier candidates, this is extended to 'calculations with bounds', where you must use the error intervals of multiple values to find the maximum or minimum possible outcome of a calculation, such as an area or a division. This topic has strong synoptic links to measurement, estimation, and algebraic manipulation, making it a crucial skill across the syllabus.
Key Concepts
Concept 1: The Anatomy of an Error Interval
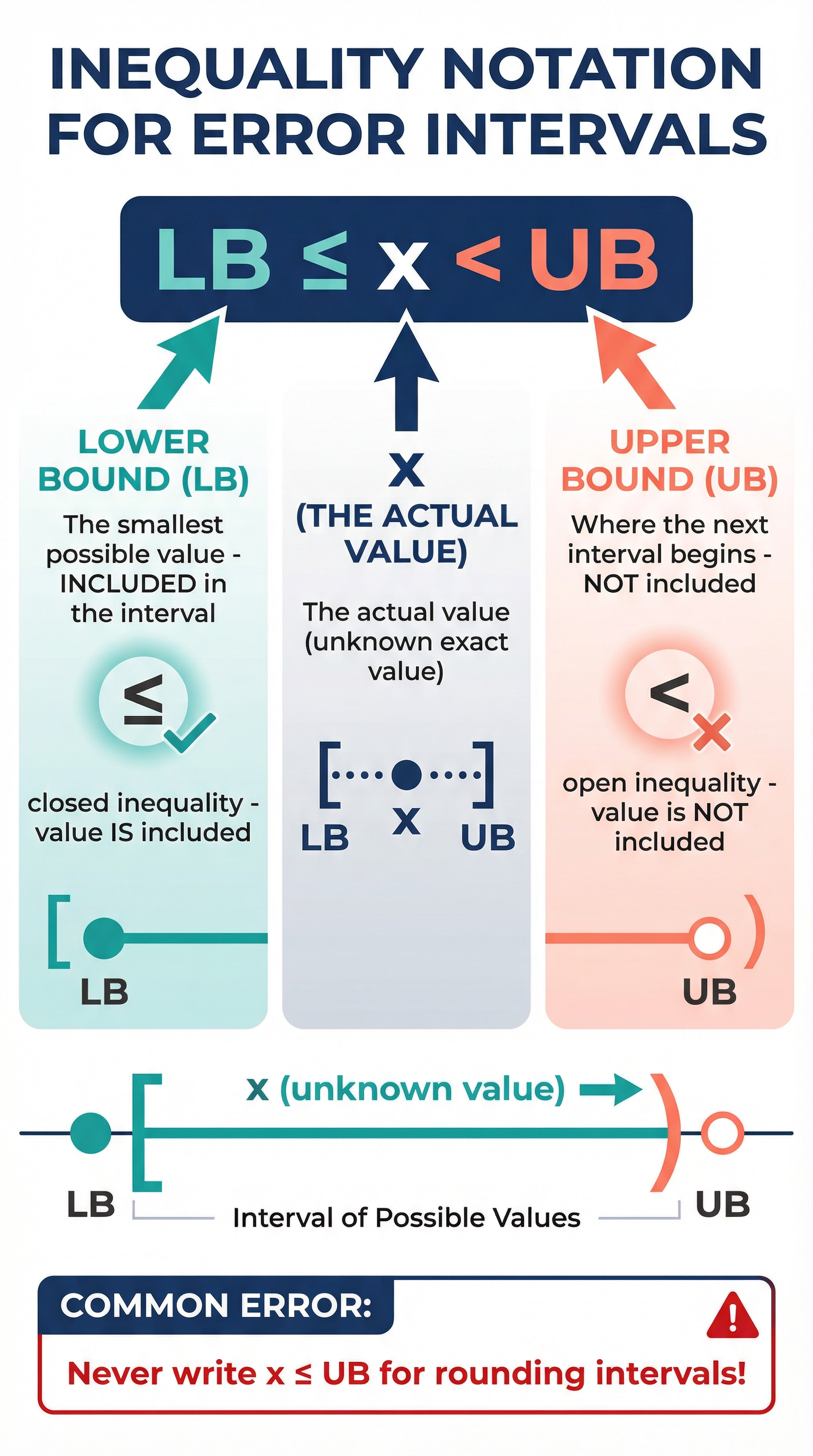
At its heart, an error interval is a statement of the range of possible values a number could have been before it was rounded or truncated. The single most important thing to memorise is the standard notation: LB ≤ x < UB.
- x: Represents the true, exact value of the number.
- LB (Lower Bound): The smallest possible value that x could have been. This value is included in the interval, hence the 'less than or equal to' symbol (≤).
- UB (Upper Bound): The value at which the next interval begins. It is the smallest value that would round up to the next number. Therefore, the true value must be strictly less than this, hence the 'less than' symbol (<).
Example: A length, l, is 6 cm to the nearest cm.
The degree of accuracy is 1 cm. We halve this to get 0.5 cm.
Lower Bound (LB) = 6 - 0.5 = 5.5 cm.
Upper Bound (UB) = 6 + 0.5 = 6.5 cm.
So, the error interval is 5.5 ≤ l < 6.5.
Concept 2: Rounding vs. Truncation
Examiners frequently test the difference between rounding and truncation. While they sound similar, they produce different error intervals.
- Rounding: Finds the nearest value. The error interval is symmetrical around the given value.
- Truncation: Simply 'chops off' digits at a certain point, ignoring the values of the digits that follow. The given value is always the Lower Bound.
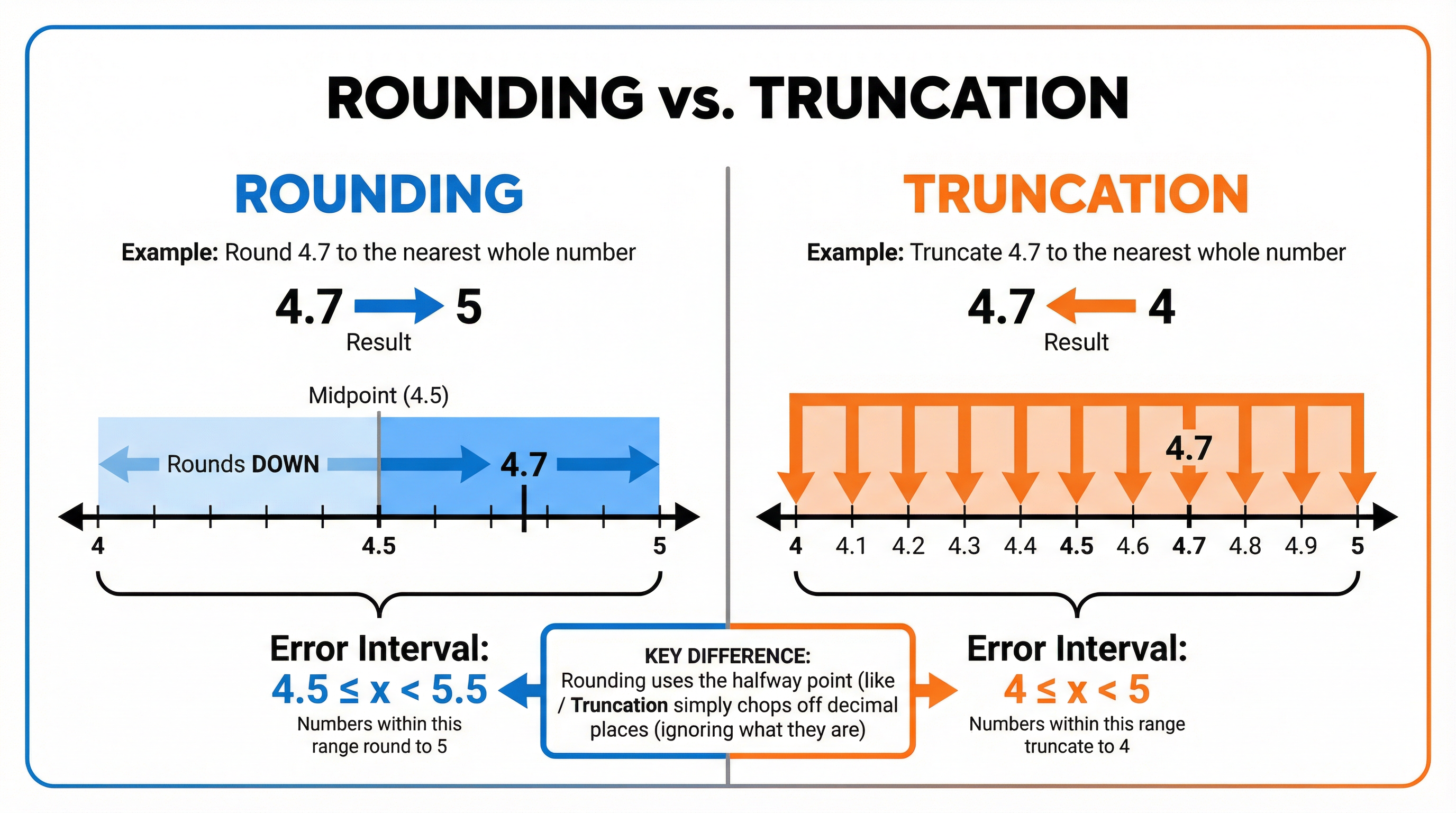
Example: A number, y, is 4.8 after being truncated to 1 decimal place.
This means the original number could have been 4.80, 4.81, 4.89, etc., but not 4.9. The original value was 'chopped' to 4.8.
Lower Bound (LB) = 4.8
Upper Bound (UB) = 4.9
So, the error interval is 4.8 ≤ y < 4.9.
Concept 3: Calculations with Bounds (Higher Tier Only)
This is where precision is paramount. To find the maximum or minimum value of a calculation involving rounded numbers, you must first find the bounds of each individual number.
Mathematical Relationships
| Operation | To Find Upper Bound (Max Value) | To Find Lower Bound (Min Value) |
|---|---|---|
| Addition (A + B) | UB(A) + UB(B) | LB(A) + LB(B) |
| Subtraction (A - B) | UB(A) - LB(B) | LB(A) - UB(B) |
| Multiplication (A x B) | UB(A) x UB(B) | LB(A) x LB(B) |
| Division (A / B) | UB(A) / LB(B) | LB(A) / UB(B) |
Crucial Note: For subtraction and division, to make the result as large as possible, you must divide/subtract by the smallest possible number. This is a common area where candidates lose marks.
Practical Applications
Error intervals are used constantly in science, engineering, and manufacturing. For example, a piston in a car engine must be a specific size, but manufacturing has tolerances. An error interval defines the acceptable range of sizes for the piston to work correctly. If it's too small (below the LB), it will rattle; if it's too large (at or above the UB), it won't fit. This ensures quality control and safety.
