Study Notes
Overview
Vectors are a fundamental concept in mathematics, representing quantities that possess both magnitude (size) and direction. Think of them as a set of instructions for movement on a grid. This topic is crucial as it forms the bedrock of mechanics, physics, and advanced geometry. In your OCR GCSE exam, you'll face questions ranging from simple vector arithmetic to challenging geometric proofs that require clear, logical reasoning. Mastering vectors not only secures marks in dedicated questions but also enhances your spatial awareness and problem-solving skills, linking directly to transformations and coordinate geometry. Expect to see questions asking you to 'Find' a resultant vector, 'Show that' two vectors are parallel, or 'Prove' that three points are collinear. This guide will equip you to handle them all.
Key Concepts
Concept 1: Vector Notation and Representation
A vector is most commonly written as a column vector. This consists of two numbers stacked vertically inside round brackets. The top number indicates movement in the x-direction (horizontal), and the bottom number indicates movement in the y-direction (vertical). A positive x-value means move right; a negative x-value means move left. A positive y-value means move up; a negative y-value means move down.
Crucial Examiner Tip: You will lose marks for incorrect notation. A column vector is NOT a fraction. Never draw a line between the two numbers. It must be written as (x y) stacked vertically.
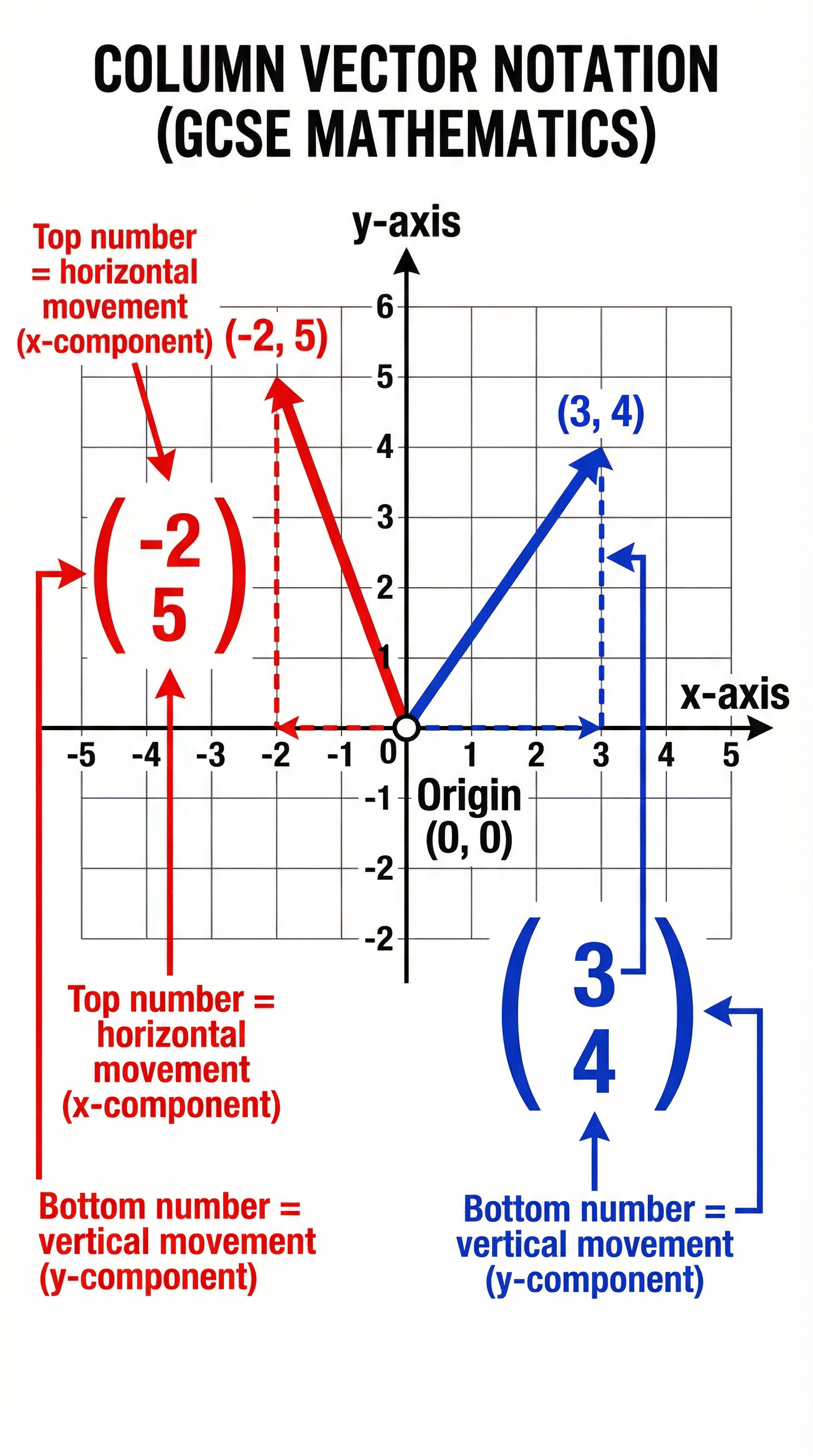
Example: The vector (3 -2) represents a movement of 3 units to the right and 2 units down.
Vectors can also be represented by a single bold letter (e.g., a) or by the start and end points with an arrow above (e.g., AB). The direction of the arrow is critical. The vector AB goes from point A to point B. The vector BA would be the exact opposite, going from B to A, and would be written as -AB or -a.
Concept 2: Vector Arithmetic
Adding and Subtracting Vectors: To add or subtract vectors, you simply add or subtract the corresponding components.
Example: If a = (2 4) and b = (1 -3), then a + b = (2+1 4-3) = (3 1).
Scalar Multiplication: A scalar is just a regular number. To multiply a vector by a scalar, you multiply each component by that scalar. This changes the vector's magnitude (length) but not its direction (unless the scalar is negative, in which case the direction is reversed).
Example: If a = (3 5), then 2a = (2*3 2*5) = (6 10). The vector 2a is twice as long as a and points in the same direction.
-3a would be (-9 -15), a vector three times as long but pointing in the opposite direction.
Concept 3: Vector Geometry and Proofs (Higher Tier)
This is where vectors become a powerful tool for proving geometric facts. You'll use vector addition and subtraction to find pathways between points.
The Triangle and Parallelogram Rules for AdditionTo get from point A to point C, you can go via point B. This creates a 'vector pathway': AC = AB + BC. This is the fundamental principle for all vector geometry.
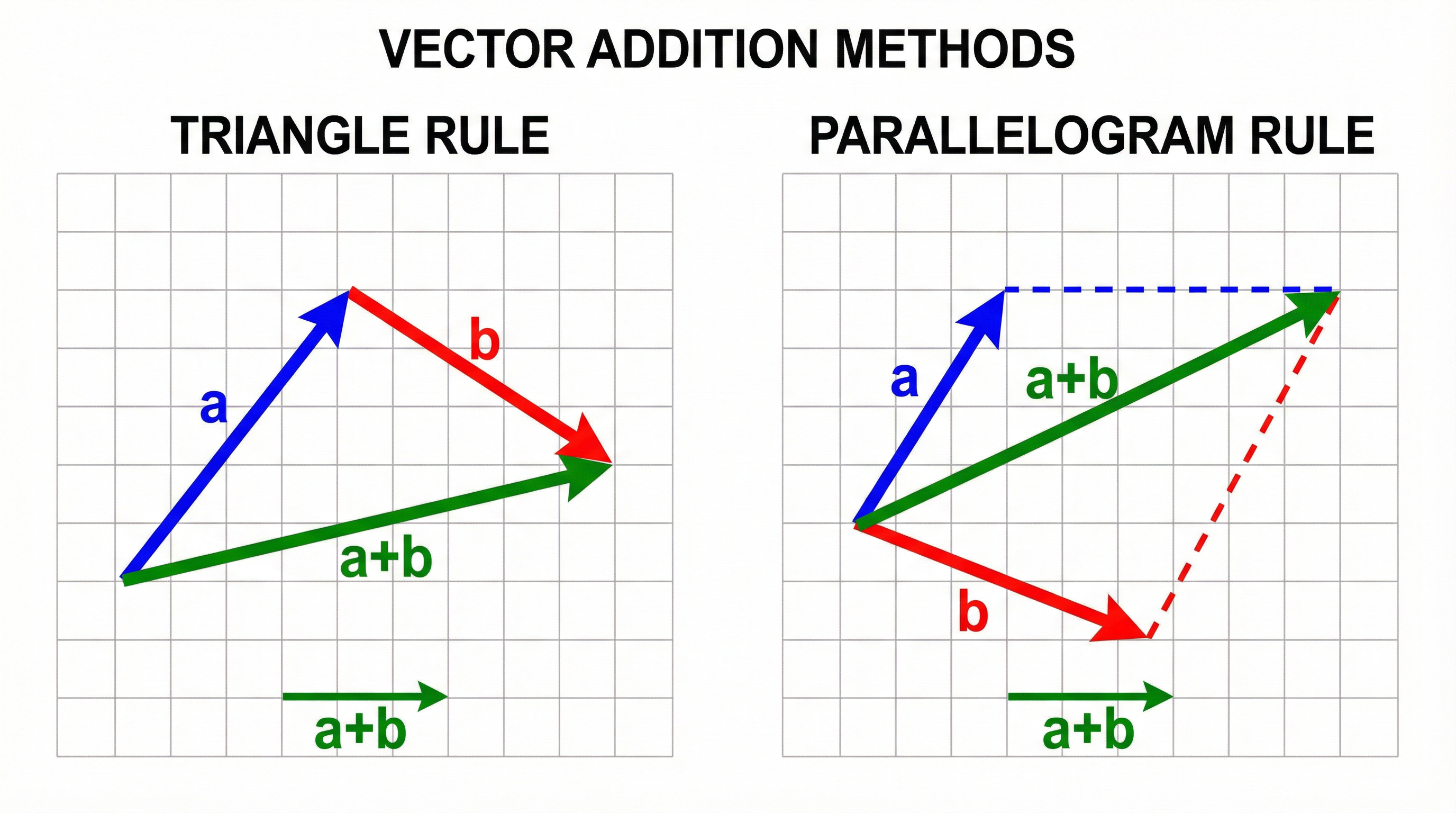
Proving Parallelism: Two vectors are parallel if one is a scalar multiple of the other. For example, if vector PQ = 2 * vector RS, then PQ is parallel to RS. The length of PQ is double the length of RS, and they travel in the same direction.
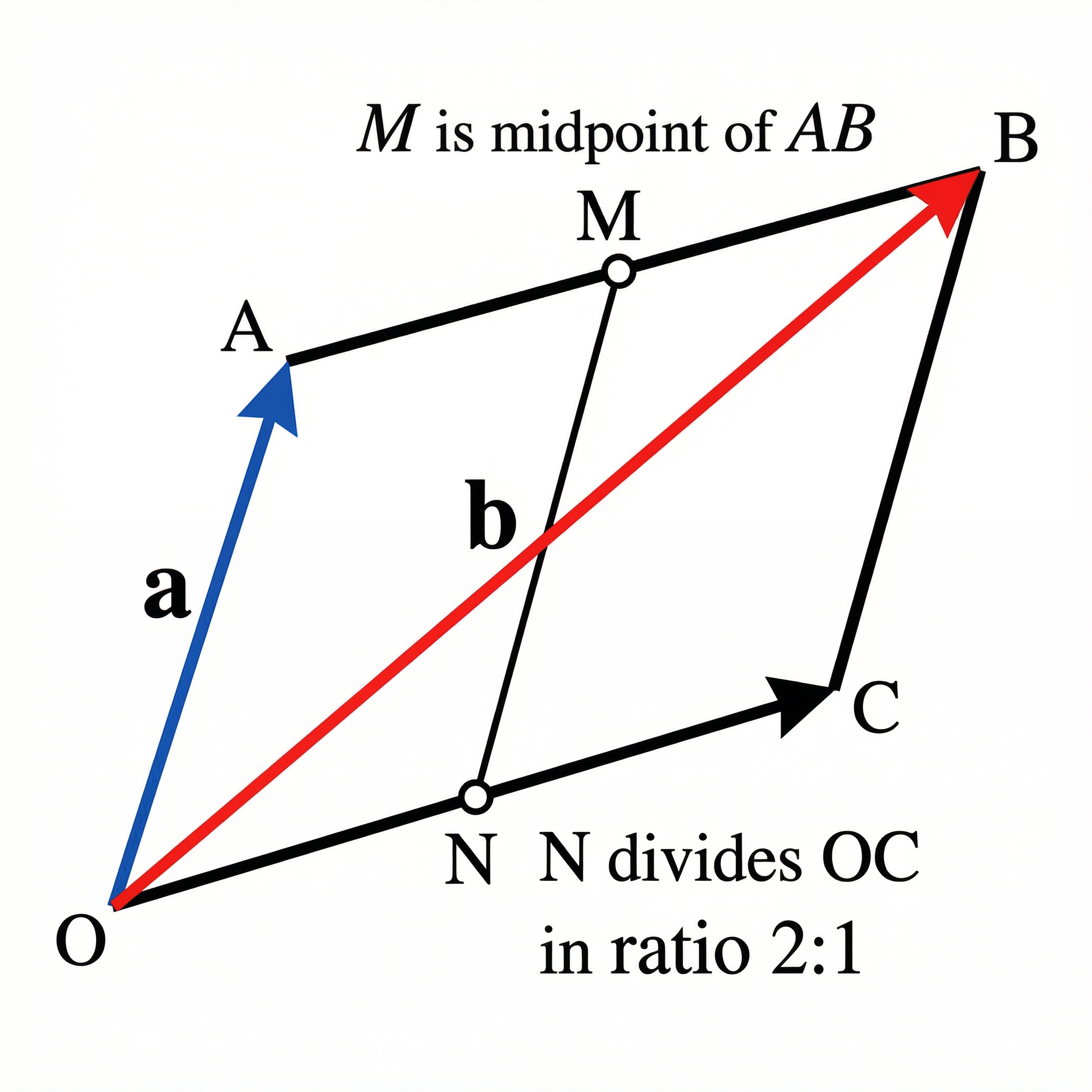
Proving Collinearity: Three points (e.g., A, B, and C) are collinear if they all lie on the same straight line. To prove this, you must show two things:
- The vectors connecting the points are parallel (e.g., AB is a scalar multiple of BC).
- They share a common point (in this case, point B).
Mathematical Relationships
Magnitude of a Vector: The magnitude (or modulus) of a vector a = (x y) is its length, written as |a|. It is calculated using Pythagoras' Theorem.
- Formula: |a| = sqrt(x² + y²)
- Status: Must memorise.
Position Vectors: A position vector is a vector that starts at the origin (O). The position vector of point A, written OA, is simply the coordinates of A written as a column vector.
Vector Subtraction for Geometry: To find the vector between two points A and B, you can use their position vectors a and b:
- Formula: AB = b - a (final point's position vector minus the initial point's position vector).
- Status: Must memorise.
Practical Applications
Vectors are essential in many real-world fields:
- Physics: Describing forces, velocity, and acceleration.
- Aviation and Navigation: Pilots and ship captains use vectors to calculate routes that account for wind or water currents.
- Computer Graphics: In video games and animation, vectors are used to determine the position, movement, and orientation of objects in 3D space.
- Engineering: Structural engineers use vectors to analyse forces on bridges and buildings to ensure they are stable.