Study Notes

Overview
Welcome to the definitive guide for AQA GCSE Mathematics topic 1.2: Fractions, Decimals, and Percentages. This topic is a cornerstone of the mathematics curriculum, forming the bedrock for a vast range of more advanced concepts. AQA places significant emphasis on this area, with questions appearing in every paper and across all assessment objectives. AO1 (Use and apply standard techniques) is heavily tested through procedural fluency in calculations and conversions, while AO3 (Solve problems and interpret solutions) is assessed via multi-step problems often set in financial or real-world contexts. For Foundation tier candidates, a solid grasp of equivalence and basic arithmetic is key. For Higher tier candidates, examiners expect mastery of more complex areas like reverse percentages, compound interest multipliers, and the algebraic conversion of recurring decimals. This guide will equip you with the knowledge, strategies, and resources to approach this topic with confidence, ensuring you can translate your understanding into marks on exam day.
Key Concepts
Concept 1: Equivalence and Conversion
Fractions, decimals, and percentages are three different ways of representing the same value. Think of them as different languages expressing the same idea. Fluency in converting between them is a fundamental skill that underpins the entire topic. Examiners will test this directly and indirectly in almost every related question.
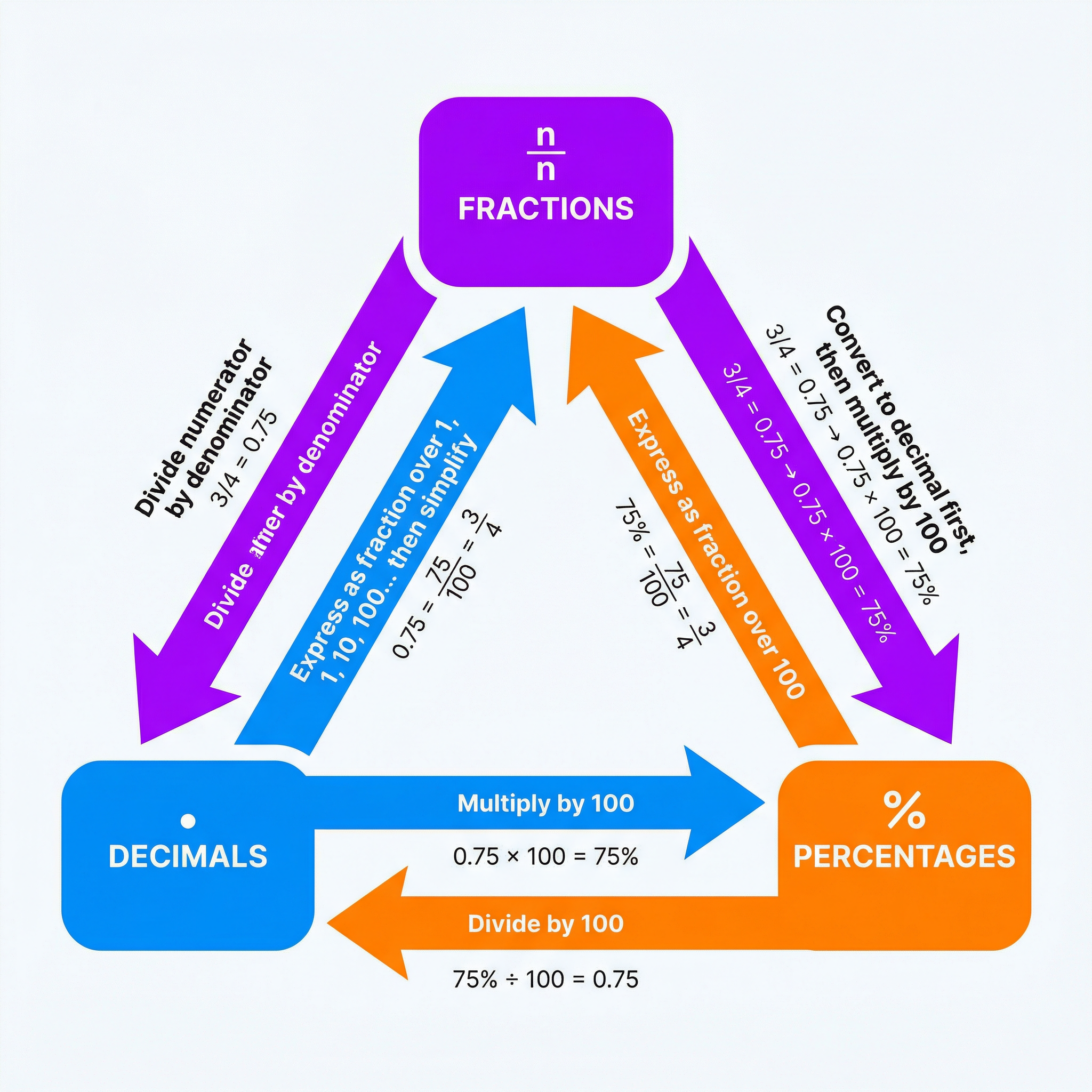
Why it works: The system is based on parts of a whole. A fraction represents a part of a whole (e.g., 3/4 is 3 parts out of 4). A decimal represents a part of a whole in base-10 (e.g., 0.75 is 75 hundredths). A percentage represents a part of a whole out of 100 (e.g., 75% is 75 out of 100). They are all interlinked.
Example: Convert 2/5 into a decimal and a percentage.
- To Decimal: Divide the numerator by the denominator: 2 ÷ 5 = 0.4
- To Percentage: Multiply the decimal by 100: 0.4 × 100 = 40%
Concept 2: Operations with Fractions
Candidates must be proficient in the four basic operations: addition, subtraction, multiplication, and division of fractions, including mixed numbers.
Addition and Subtraction: The non-negotiable rule is to find a common denominator. This means finding a common multiple of the denominators of the fractions you are adding or subtracting. You cannot simply add or subtract the denominators – a very common mistake that scores zero marks.
Example: Calculate 2/3 + 1/5.
- Find a common denominator: The lowest common multiple of 3 and 5 is 15.
- Convert the fractions: 2/3 = 10/15 and 1/5 = 3/15.
- Add the numerators: 10/15 + 3/15 = 13/15.
Multiplication: This is more straightforward. Multiply the numerators together and multiply the denominators together. Always check if you can simplify the result.
Example: Calculate 3/4 × 2/7.
- Multiply numerators: 3 × 2 = 6
- Multiply denominators: 4 × 7 = 28
- Result: 6/28, which simplifies to 3/14.
Division: Use the 'Keep, Change, Flip' (KCF) method. Keep the first fraction, change the division sign to multiplication, and flip the second fraction (find its reciprocal).
Example: Calculate 4/5 ÷ 2/3.
- Keep: 4/5
- Change: ÷ to ×
- Flip: 2/3 to 3/2
- Calculation: 4/5 × 3/2 = 12/10, which simplifies to 6/5 or 1 1/5.
Concept 3: Percentage Change and Multipliers
This is a high-frequency exam topic, especially in AO3 problem-solving. The multiplier method is the most efficient and examiner-friendly technique.

Why it works: A percentage increase or decrease is a change from an original 100%. By calculating the new percentage (e.g., 100% + 15% = 115%) and converting it to a decimal (1.15), you create a single multiplier that performs the entire calculation in one step.
Percentage Increase: Add the percentage increase to 100% and convert to a decimal.
Example: Increase £60 by 12%.
- New percentage: 100% + 12% = 112%
- Multiplier: 1.12
- Calculation: £60 × 1.12 = £67.20
Percentage Decrease: Subtract the percentage decrease from 100% and convert to a decimal.
Example: Decrease 150kg by 30%.
- New percentage: 100% - 30% = 70%
- Multiplier: 0.70 or 0.7
- Calculation: 150kg × 0.7 = 105kg
Concept 4: Reverse Percentages (Higher Tier)
This involves finding the original value after a percentage change has occurred. It is a classic Higher tier question that catches many candidates out. The key is to understand that the final value represents a percentage of the original, and you must divide to reverse the change.
Example: A coat is in a sale with 20% off. The sale price is £96. What was the original price?
- The sale price represents 100% - 20% = 80% of the original price.
- The multiplier was 0.8.
- To reverse this, we divide by the multiplier: £96 ÷ 0.8 = £120.
- A common error is to calculate 20% of £96 and add it on, which is incorrect and scores no marks.
Concept 5: Recurring Decimals to Fractions (Higher Tier)
This is a proof-based question that requires clear algebraic manipulation. You must show every step of your working to be awarded full marks.
Example: Show that the recurring decimal 0.272727... can be written as the fraction 3/11.
- Step 1: Let x = 0.272727...
- Step 2: We need to move the decimal point past one full repeating cycle. The cycle is '27', which is two digits long, so we multiply by 100.
100x = 27.272727... - Step 3: Subtract the original equation (x) from the new one (100x) to eliminate the recurring part.
100x - x = 27.272727... - 0.272727...
99x = 27 - Step 4: Solve for x and simplify.
x = 27/99
x = 3/11 (dividing top and bottom by 9)
Mathematical/Scientific Relationships
- Fraction to Decimal: Numerator ÷ Denominator
- Decimal to Percentage: Decimal × 100
- Percentage to Decimal: Percentage ÷ 100
- Percentage Change Multiplier (Increase): 1 + (Percentage / 100)
- Percentage Change Multiplier (Decrease): 1 - (Percentage / 100)
- Reverse Percentage: Final Amount ÷ Multiplier
- Compound Interest/Growth Formula: Final Value = Principal × (Multiplier)^n (where n is the number of periods). This is a crucial formula that you Must memorise for the Higher tier.
Practical Applications
This topic is deeply rooted in real-world mathematics. Examiners frequently use these contexts to test AO3 skills:
- Finance: Calculating interest (simple and compound), profit and loss, tax (VAT), and discounts.
- Statistics: Representing data as fractions or percentages of a whole in pie charts and tables.
- Science: Calculating percentage yield in chemistry or percentage error in physics experiments.
- Everyday Life: Adjusting recipes, calculating fuel consumption, or understanding nutritional information on food packaging.
