Loci

Overview

A locus is a set of points that satisfies a specific rule or condition. In your AQA GCSE exam, this topic tests your ability to accurately construct geometric paths and regions using a ruler and compasses. It’s a highly visual topic that combines pure mathematical skill with practical problem-solving, often involving scale drawings and maps. Mastering the four key constructions is crucial for securing marks, as these skills form the foundation for more complex questions where you must identify regions that satisfy multiple conditions simultaneously. This topic has strong synoptic links to Geometry, Measures, and Graphical Transformations, making it a vital part of the syllabus.

Key Concepts

Concept 1: Locus of points at a fixed distance from a point

This is the most fundamental locus. The set of all points that are a fixed distance from a central point, P, forms a circle with P as its centre. Think of it as the path a dog on a leash can take around a pole it's tied to. The length of the leash is the radius of the circle.

Why it works: A circle is defined as the set of all points in a plane that are at a given distance from a given point, the centre. The compass is the perfect tool for this, as its fixed width ensures every point on the curve you draw is exactly the same distance from the centre point.

Example: To construct the locus of points 3cm from a point X, you set your compass radius to 3cm, place the point on X, and draw a full circle. Every single point on the circumference of this circle is exactly 3cm away from X.

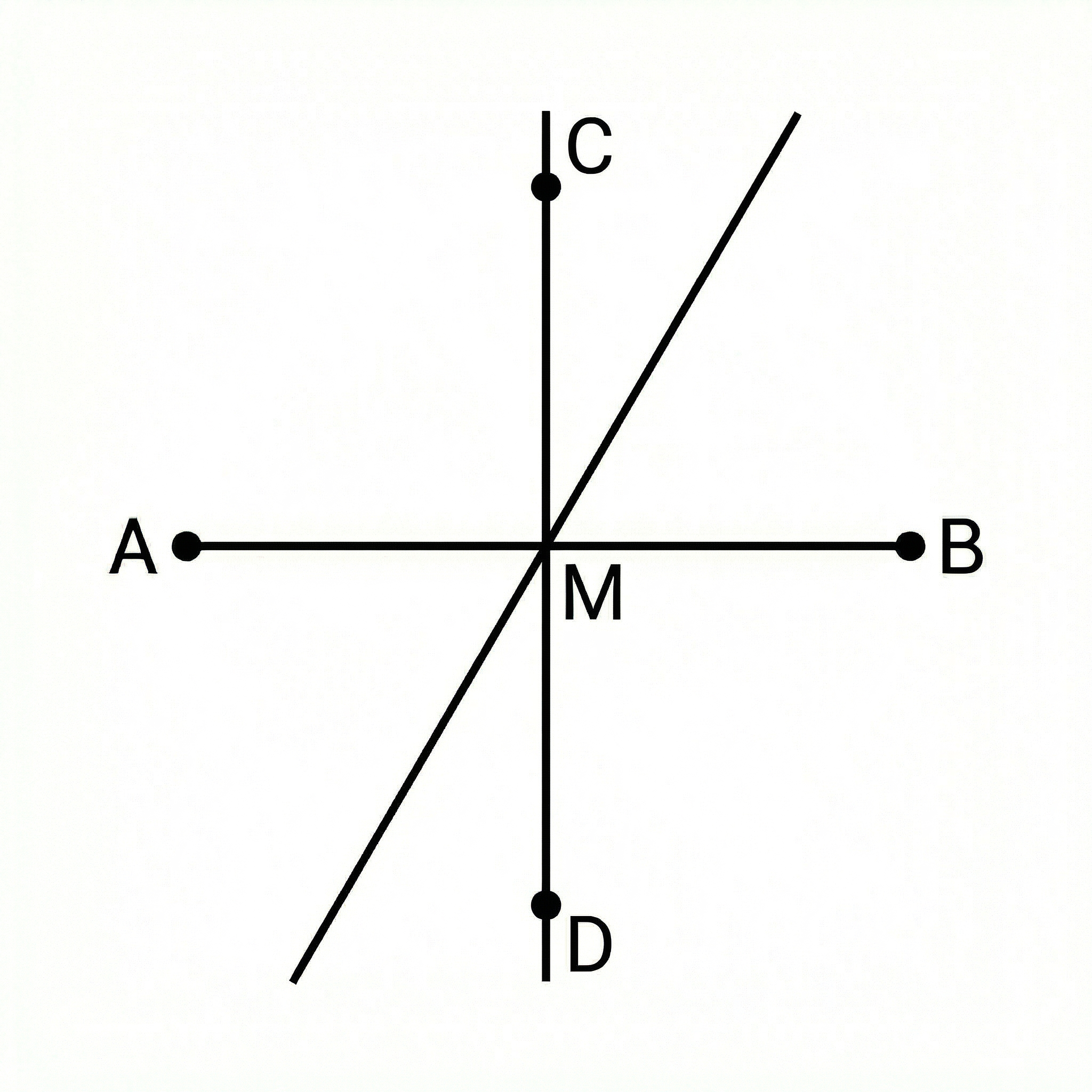
Concept 2: Locus of points equidistant from two fixed points

This locus forms a straight line that is the perpendicular bisector of the line segment connecting the two points. Imagine two friends, A and B, standing in a park. The line of points where you would be the exact same distance from both of them is the perpendicular bisector of the line AB.

Why it works: By using intersecting arcs of the same radius from both points (A and B), you create points of intersection that are, by definition, equidistant from A and B. A straight line drawn through these intersection points maintains this property along its entire length. This construction creates two congruent right-angled triangles, proving the line is both perpendicular and bisects the original segment.

Example: To find the locus of points equidistant from points C and D, you open your compass to a width that is clearly more than half the distance between C and D. You swing an arc from C, then swing another arc of the same radius from D so they intersect. You repeat this on the other side of the line CD and draw a straight line through the two points where the arcs cross.

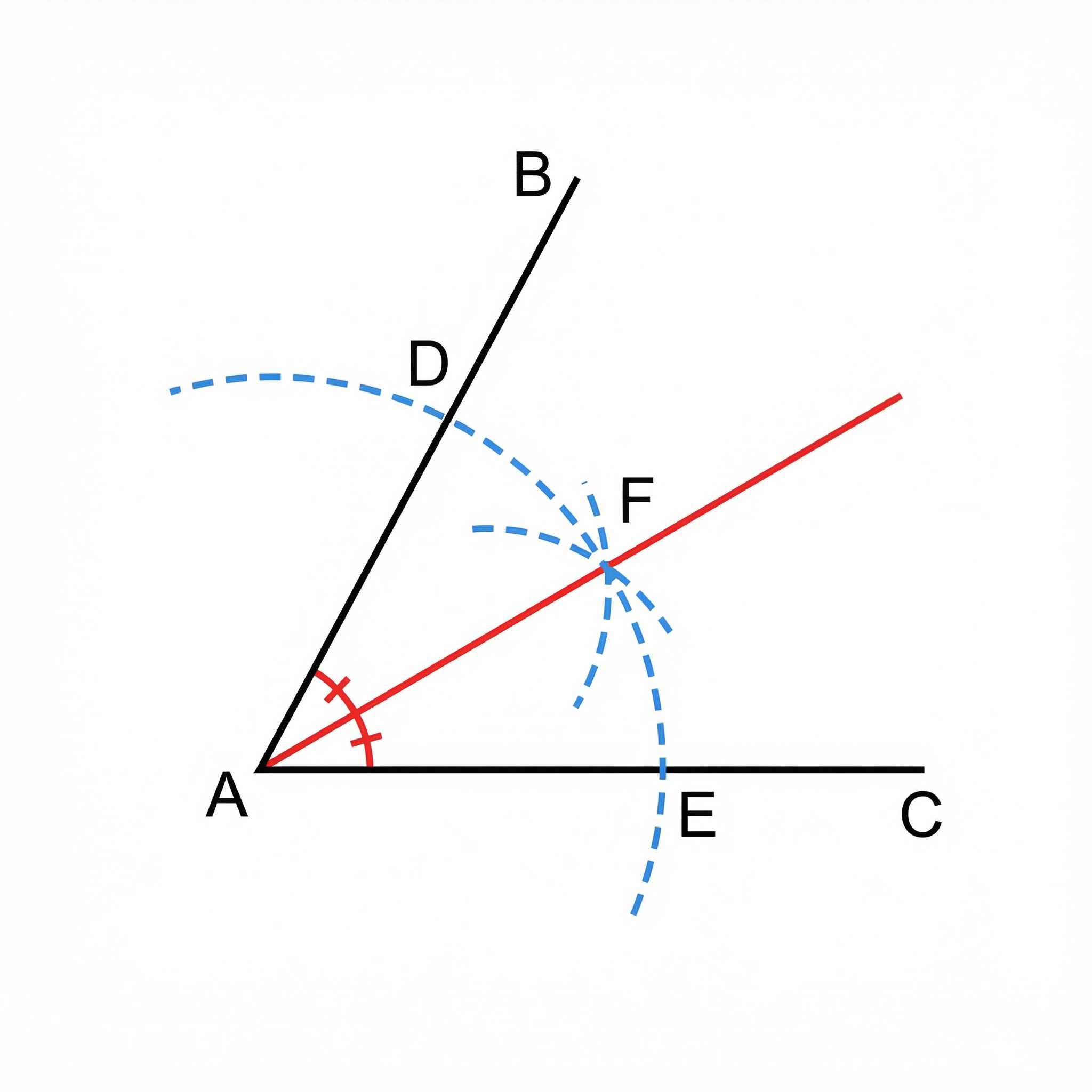
Concept 3: Locus of points equidistant from two intersecting lines

This locus is the angle bisector of the angle formed by the two lines. It's a straight line that splits the angle perfectly in two. Think of it as the path you'd walk to stay exactly in the middle of two converging paths.

Why it works: The construction involves creating two points (P and Q) on the arms of the angle that are equidistant from the vertex. The subsequent intersecting arcs from P and Q create a point that is equidistant from both P and Q, and therefore equidistant from the two lines themselves. A line from the vertex through this point will always be in the middle.

Example: To bisect an angle, you place your compass point on the vertex (where the two lines meet) and draw an arc that crosses both lines. Then, from each of these intersection points, you draw two more arcs of equal radius in the middle of the angle. A line from the vertex through the point where these arcs cross is the angle bisector.

Concept 4: Locus of points at a fixed distance from a line

This locus consists of two parallel lines, one on each side of the original line, at the specified distance. Imagine a straight train track; the locus of points 2 metres away from the track would be two new lines running parallel to it, one on each side.

Why it works: A line has infinite length, so the locus of points a fixed distance from it must also extend infinitely in a parallel direction. The ends are typically capped with semi-circles if the original line is a finite line segment.

Example: To construct the locus of points 2cm from a line segment EF, you would draw two lines parallel to EF, each 2cm away. You would then use a compass set to 2cm, place the point on E and F, and draw semi-circles at each end to connect the parallel lines. This creates a 'running track' shape.

Mathematical/Scientific Relationships

There are no complex formulas to memorise for Loci, as it is a topic of geometric construction. The key relationships are the geometric properties themselves:

• Circle Equation (Higher Tier Link): The locus of points (x, y) at a distance 'r' from a centre (a, b) is given by the equation (x-a)² + (y-b)² = r². This is not typically required for construction but is a key synoptic link to coordinate geometry.
• Pythagoras' Theorem: Can be used to verify distances in right-angled triangles formed by loci, especially with perpendicular bisectors.

Practical Applications

Loci are used extensively in real-world design, engineering, and planning:

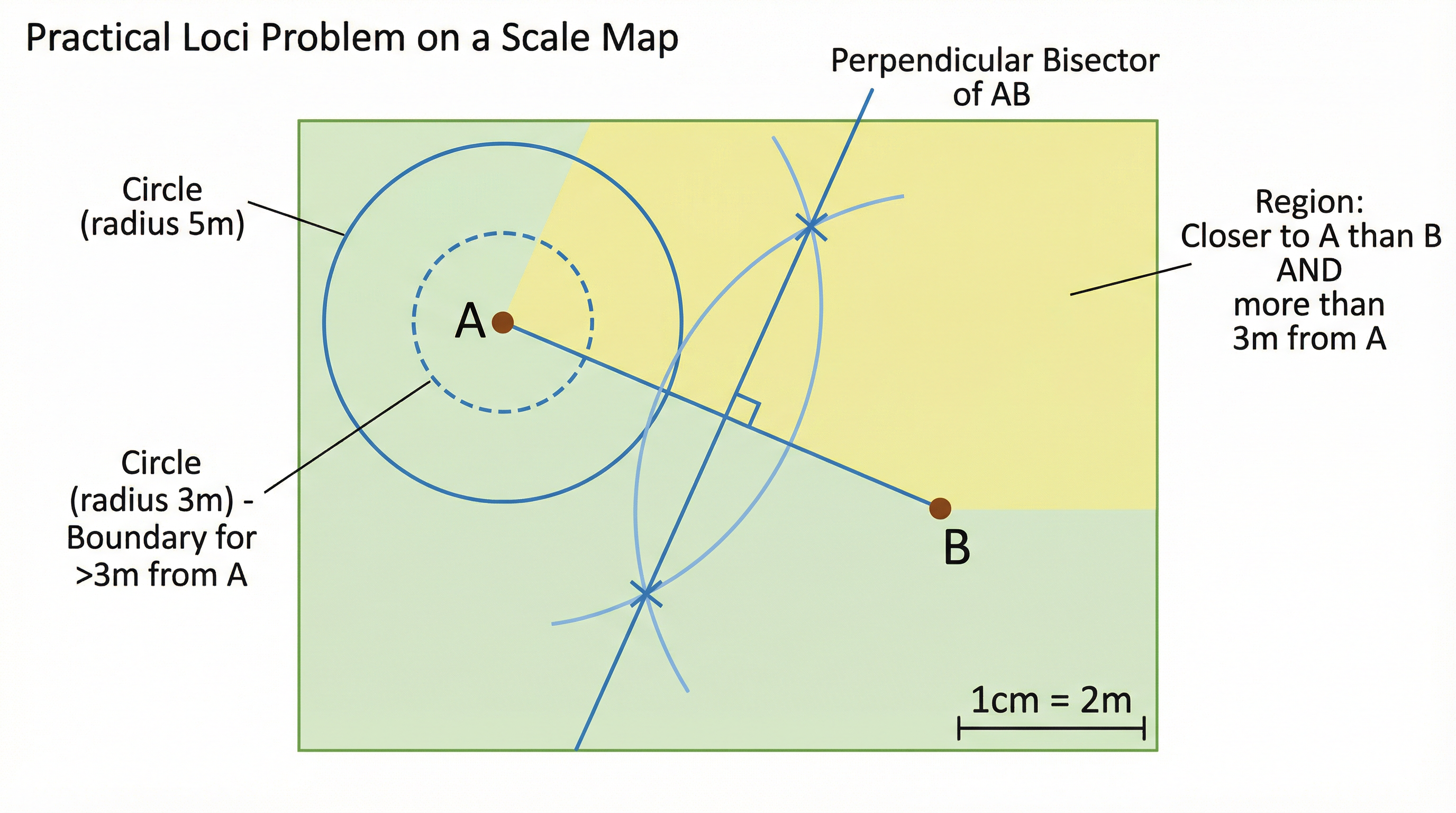
• Mobile Phone Masts: To ensure signal coverage, a mobile phone company needs to find the optimal position for a new mast. They might need it to be within a certain range of a town (a circular locus) but also closer to Town A than Town B (a perpendicular bisector locus).
• Robotics: A robot vacuum cleaner uses loci principles to navigate a room, staying a certain distance from walls (parallel line locus) and navigating around furniture (circular loci).
• Air Traffic Control: Flight paths are planned to maintain a safe distance from each other, using loci to define corridors in the sky.