Study Notes

Overview
Proportion is a fundamental concept in mathematics that describes how quantities relate and change with respect to each other. For your AQA GCSE exam, this isn't just about simple scaling; it's about building mathematical models. You'll be expected to translate real-world scenarios into algebraic formulas, solve for unknown values, and interpret the graphical representations of these relationships. From Foundation tier questions on recipe scaling and currency conversion to Higher tier challenges involving inverse square laws in science, a solid grasp of proportion is essential. It's a topic that links heavily with algebra, graphs, and problem-solving, making it a favourite for examiners looking to test your deeper understanding of mathematical principles. Mastering the techniques in this guide will not only prepare you for specific proportion questions but also enhance your skills across the entire specification.
Key Concepts
Concept 1: Direct Proportion
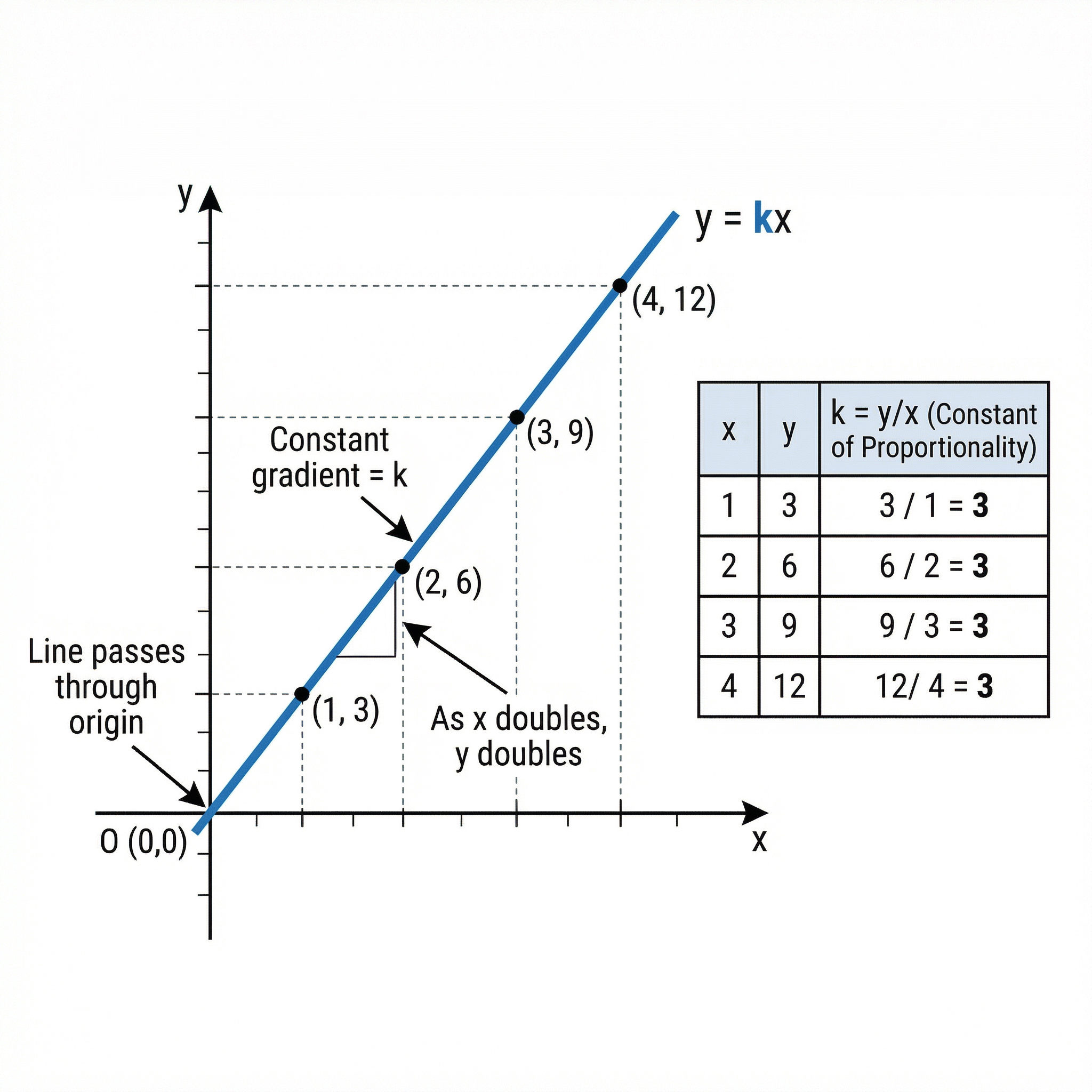
Direct proportion is a relationship where two quantities increase or decrease at the same constant rate. If you buy more, you pay more. If you use less, you need less. The key is the 'constant rate'. We represent this relationship with the formula y = kx, where 'k' is the constant of proportionality. It's the 'magic number' that connects x and y. To find 'k', you simply rearrange the formula to k = y/x.
Example: The cost of petrol is directly proportional to the volume bought. If 10 litres cost £15, what is the formula connecting cost (C) and volume (V)?
- Step 1: Write the relationship: C = kV
- Step 2: Substitute the known values to find k: 15 = k * 10
- Step 3: Solve for k: k = 15 / 10 = 1.5
- Step 4: Write the final formula: C = 1.5V. This formula can now be used to find the cost for any volume, or the volume for any cost.
Concept 2: Inverse Proportion
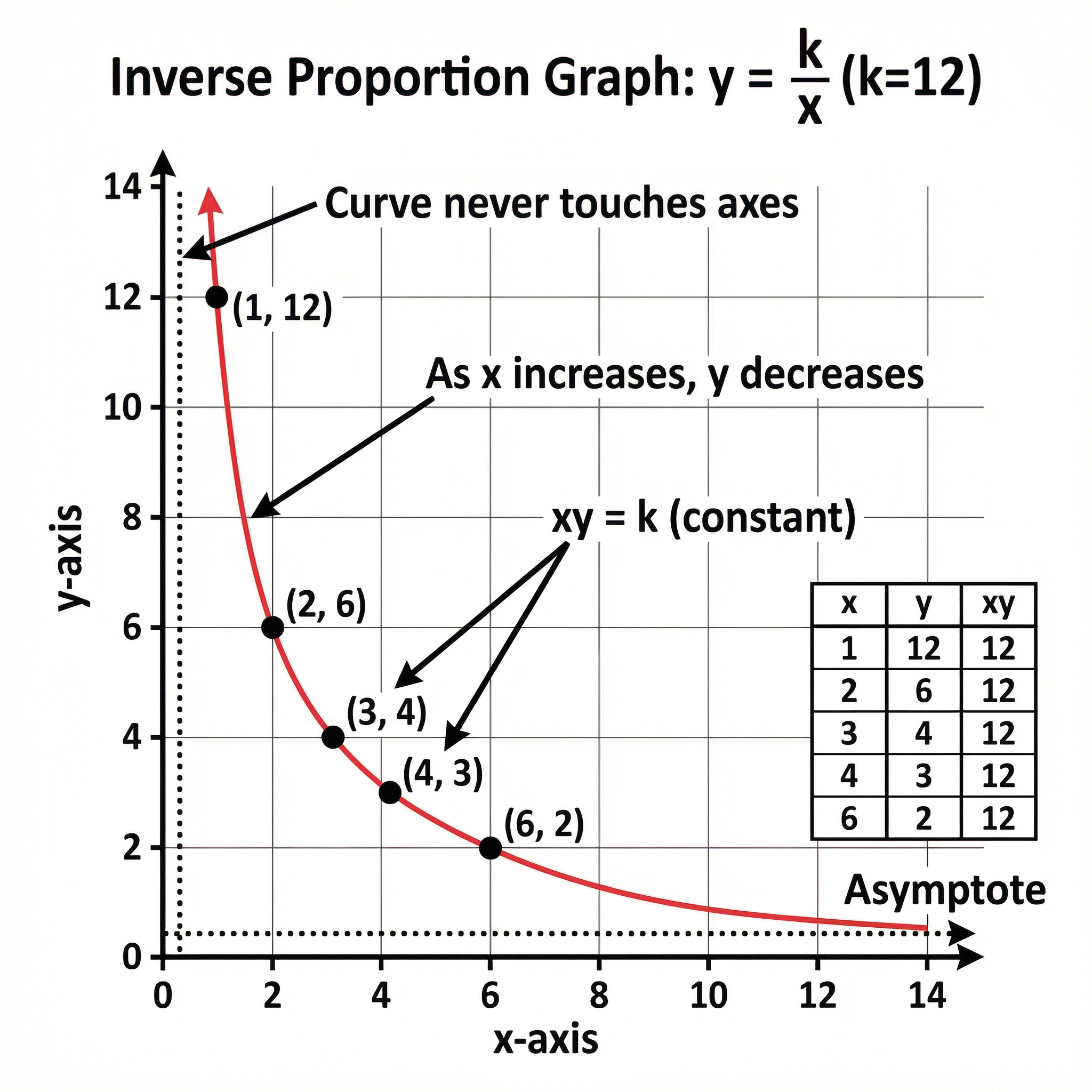
Inverse proportion is the opposite. As one quantity increases, the other quantity decreases. Think about speed and time. The faster you go, the less time the journey takes. The core formula is y = k/x or xy = k. This shows that the product of the two quantities is always constant. If you double one, you must halve the other to keep the product the same.
Example: The time (T) taken to dig a trench is inversely proportional to the number of workers (W). If it takes 2 workers 8 hours, how long would it take 4 workers?
- Step 1: Write the relationship: T = k/W
- Step 2: Substitute to find k: 8 = k / 2, so k = 16. The constant represents the total 'worker-hours' needed for the job.
- Step 3: Write the final formula: T = 16/W
- Step 4: Use the formula for the new situation: T = 16 / 4 = 4 hours. It makes sense: double the workers, half the time.
Concept 3: Proportion and Powers (Higher Tier)
At the Higher tier, the relationships become more complex. You'll encounter proportion involving squares, cubes, or roots. For example, the area of a circle is directly proportional to the square of its radius (A = πr²), where k = π. A common exam question involves scientific contexts, like gravitational force.
Example: The force of gravity (F) between two objects is inversely proportional to the square of the distance (d) between them. This is written as F = k/d². This means if you double the distance, the force becomes four times weaker (because 2² = 4). If you triple the distance, the force is nine times weaker. This 'inverse square' relationship is a critical concept in physics and a challenging type of proportion question.
Mathematical Relationships
| Relationship Type | Formula (General) | Formula (to find k) | Graph Shape | Key Feature | Tier |
|---|---|---|---|---|---|
| Direct Proportion | y = kx | k = y/x | Straight line through origin | Constant ratio | Both |
| Inverse Proportion | y = k/x | k = xy | Hyperbolic curve | Constant product | Both |
| Direct to Square | y = kx² | k = y/x² | Parabolic curve through origin | y changes with the square of x | Higher |
| Inverse to Square | y = k/x² | k = yx² | Steeper hyperbolic curve | y changes with the inverse square of x | Higher |
| Direct to Square Root | y = k√x | k = y/√x | Curve from origin, less steep than y=kx | y changes with the square root of x | Higher |
Formulas to Memorise: All the general forms (y=kx, y=k/x, etc.) must be memorised. They are not given on the formula sheet.
Practical Applications
- Recipes: Scaling ingredients up or down for different numbers of people is a classic direct proportion problem.
- Currency Exchange: Converting money between currencies uses a direct proportion relationship (e.g., £1 = $1.25).
- Best Buys: Comparing products to find the best value for money involves calculating a unit cost (e.g., price per gram), which is a proportion problem.
- Physics: Many laws of physics are expressed as proportions, such as Force = Mass x Acceleration (direct), Pressure = Force / Area (inverse), and the inverse square law for gravity and light intensity.
- Map Scales: The scale on a map is a direct proportion between the distance on the map and the distance in real life.
