Ratio

Overview

Ratio (AQA specification reference 1.12) is a fundamental concept in mathematics that appears across both Foundation and Higher tier papers. It is the language we use to compare quantities, forming the bedrock of skills required for scaling recipes, interpreting maps, and even understanding financial markets. For your GCSE, mastering ratio is not just about learning a single skill; it is about unlocking the ability to solve complex, multi-step problems that link to other areas of maths like fractions, percentages, geometry, and algebra. Examiners frequently use ratio as a tool to test a candidate's ability to deconstruct a problem and apply a logical, structured method. A typical exam question might involve sharing a quantity, scaling ingredients, comparing value for money, or, at Higher tier, combining different ratios or solving for unknown variables. This guide will equip you with the precise techniques and conceptual understanding needed to approach any ratio problem with confidence.

Key Concepts

Concept 1: What is a Ratio?

A ratio is a comparison of the size of two or more quantities. It is written using a colon (:) and describes a part-to-part relationship. For example, if a bag contains 4 red sweets and 5 blue sweets, the ratio of red to blue sweets is 4:5. It is crucial to distinguish this from a fraction. The fraction of red sweets is 4/9 (part-to-whole), whereas the ratio 4:5 compares one part (red) to another part (blue). This distinction is a common source of error for many candidates.

Example: In a class, the ratio of boys to girls is 3:2. This means for every 3 boys, there are 2 girls. The total number of 'parts' is 3 + 2 = 5. So, 3/5 of the class are boys and 2/5 are girls.

Concept 2: Simplifying Ratios

Examiners expect ratios to be given in their simplest form, unless the question states otherwise. This is an easy mark to gain, but also an easy one to lose. To simplify a ratio, you must find the highest common factor (HCF) of all the numbers in the ratio and divide each part by it.

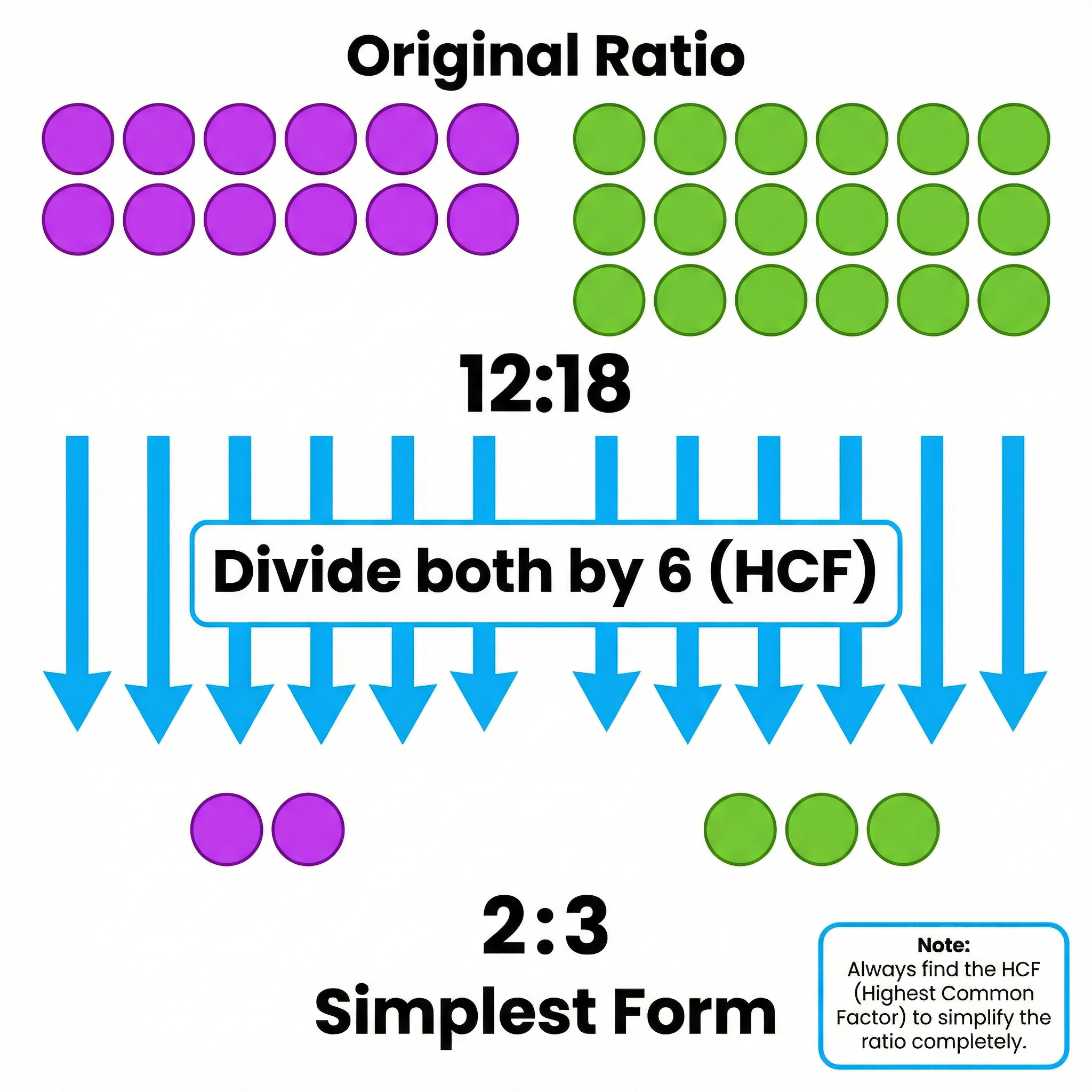
Example: To simplify the ratio 24:36, we find the HCF of 24 and 36, which is 12.

• 24 ÷ 12 = 2
• 36 ÷ 12 = 3
  So, the simplified ratio is 2:3. Credit is given for showing a correct division, even if the HCF is not used initially (e.g., dividing by 2, then 2 again, then 3).

Concept 3: Sharing a Quantity in a Given Ratio

This is one of the most common exam question styles. You are given a total amount and asked to divide it according to a specific ratio. The method is straightforward and consistently earns marks if followed correctly.

The Unitary Method:

1. Add the parts: Sum the numbers in the ratio to find the total number of parts.
2. Find one part: Divide the total quantity by the total number of parts. This gives you the value of one 'unit' or 'part'.
3. Multiply: Multiply the value of one part by each number in the original ratio to find the value of each share.

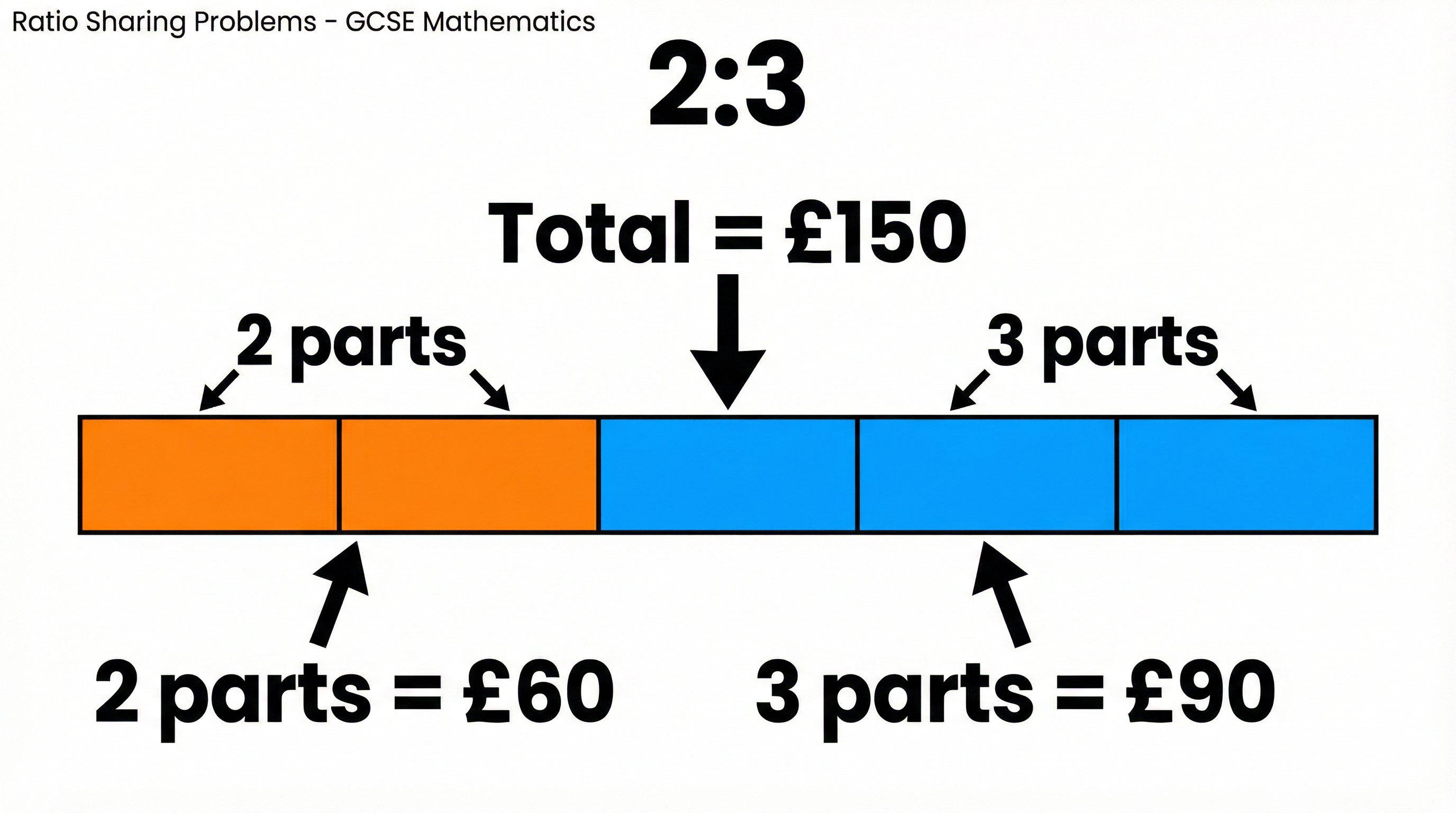
Example: Share £80 in the ratio 3:7.

1. Total parts = 3 + 7 = 10
2. Value of one part = £80 ÷ 10 = £8
3. The shares are: 3 x £8 = £24 and 7 x £8 = £56. (Check: £24 + £56 = £80)

Concept 4: Ratios in the form 1:n or n:1

This form is used to make comparisons easier, often in 'best buy' questions or on maps. To express a ratio in the form 1:n, you must make the first number 1 by dividing both sides by that first number. The same logic applies for n:1, where you divide both sides by the second number.

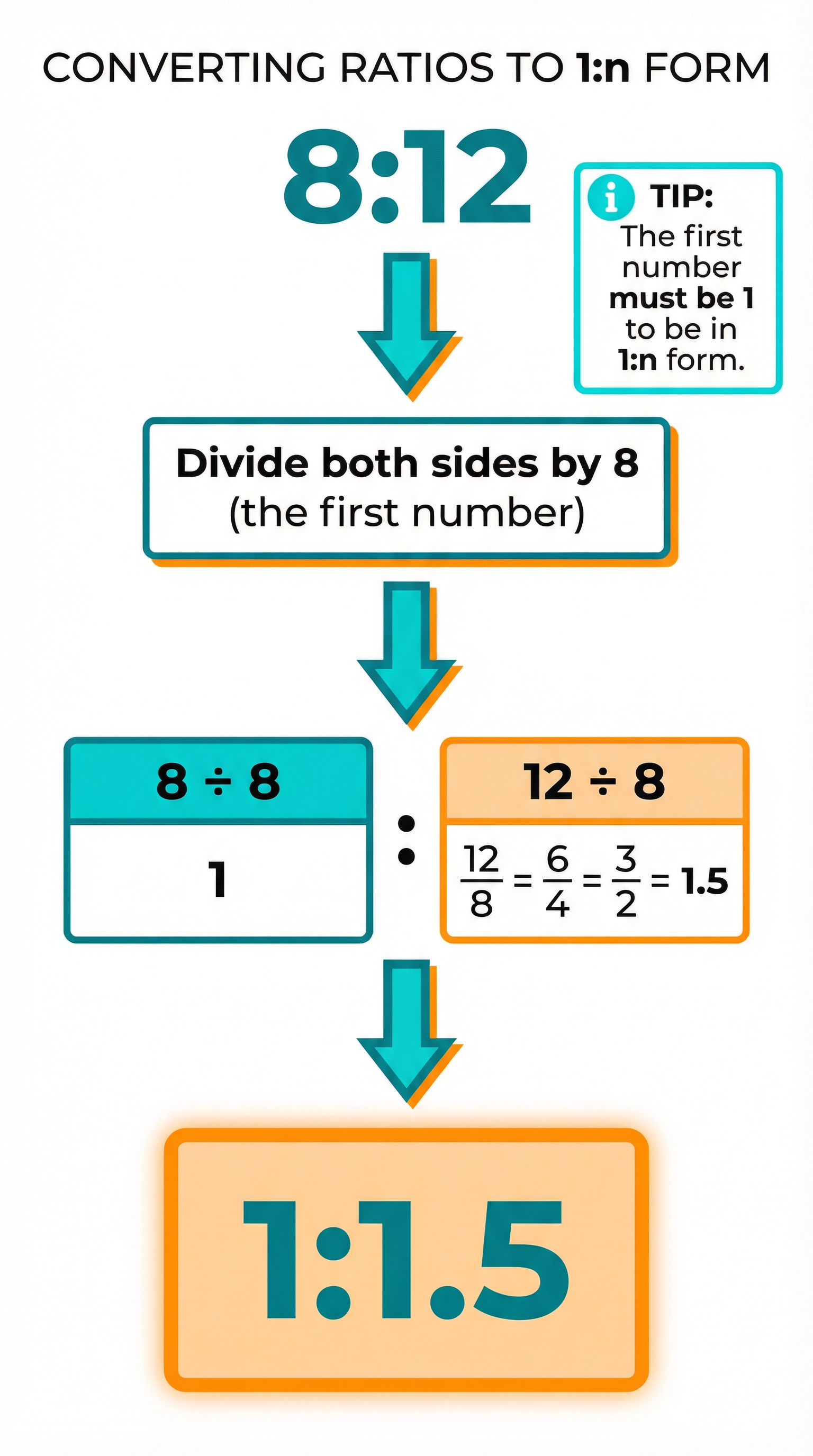
Example: Write the ratio 5:8 in the form 1:n.

• Divide both sides by 5.
• (5 ÷ 5) : (8 ÷ 5)
• The result is 1:1.6.
  Candidates must be comfortable with 'n' being a decimal or fraction and should not round it unless explicitly instructed to do so.

Concept 5: Combining Ratios (Higher Tier)

At Higher tier, candidates may be asked to combine two separate ratios that share a common element. For instance, if you know the ratio of a:b and b:c, you can find the single ratio a:b:c.

Method:

1. Identify the common element (in this case, 'b').
2. Find the lowest common multiple (LCM) of the values for the common element in both ratios.
3. Scale up each ratio so that the common element is equal to the LCM.
4. Combine the results into a single ratio.

Example: Given a:b = 2:3 and b:c = 4:5. Find a:b:c.

1. The common element is 'b', with values 3 and 4.
2. The LCM of 3 and 4 is 12.
3. Scale the first ratio: multiply by 4 to get a:b = 8:12. Scale the second ratio: multiply by 3 to get b:c = 12:15.
4. Now that 'b' is 12 in both, we can combine them: a:b:c = 8:12:15.

Mathematical Relationships

• Ratio to Fraction Conversion: In a ratio a:b, the total number of parts is a + b. The fraction for the first quantity is a/(a+b) and for the second is b/(a+b).
• Algebraic Ratios (Higher Tier): If x:y = a:b, this can be written as the equation x/y = a/b. This allows for algebraic manipulation, such as cross-multiplication to get bx = ay. This is a vital skill for solving simultaneous equations involving ratios.

Practical Applications

Ratio is not just an abstract concept; it is used everywhere in the real world, which is why it is tested so heavily.

• Cooking and Recipes: Scaling a recipe up or down requires you to multiply all ingredients by the same factor, keeping the ratios of ingredients constant.
• Maps and Scale Drawings: The scale on a map (e.g., 1:50,000) is a ratio that tells you how a distance on the map relates to the actual distance in real life.
• Business and Finance: Ratios are used to analyse company performance, such as the debt-to-equity ratio.
• Science: Mixing chemicals for an experiment requires precise ratios to ensure the correct reaction occurs.