Simultaneous equations

Overview

Simultaneous equations are a cornerstone of algebra, frequently appearing on both Foundation and Higher tier AQA GCSE Mathematics papers. This topic involves finding a set of values for two or more variables that satisfy multiple equations at the same time. In essence, you are finding the unique point of intersection where two different mathematical stories meet. For linear equations, this is the single coordinate where two straight lines cross on a graph. For Higher tier candidates, this extends to finding where a straight line intersects a curve, such as a parabola, which can result in up to two points of intersection. A strong grasp of this topic is not only crucial for direct questions, which can be worth up to 6 marks, but it also provides a foundation for more advanced mathematical concepts, including coordinate geometry and modelling real-world scenarios.

Key Concepts

Concept 1: Solving by Elimination

The elimination method is a powerful algebraic technique used to solve a pair of linear simultaneous equations. The core principle is to eliminate one of the variables by adding or subtracting the two equations. This is possible when the coefficients of one of the variables are either the same or are additive inverses (e.g., +3y and -3y). If the coefficients are not initially helpful, you must first multiply one or both equations by a constant to create this condition. Once a variable is eliminated, you are left with a simple one-variable equation to solve. The value of this first variable is then substituted back into one of the original equations to find the value of the second variable.

Example: Consider the equations 3x + 2y = 16 and 2x - 2y = 4. Notice the coefficients of y are +2 and -2. By adding the two equations together, the y terms are eliminated: (3x + 2x) + (2y - 2y) = 16 + 4, which simplifies to 5x = 20. Solving for x gives x = 4. Substituting x = 4 into the first equation gives 3(4) + 2y = 16, so 12 + 2y = 16, leading to 2y = 4 and finally y = 2.

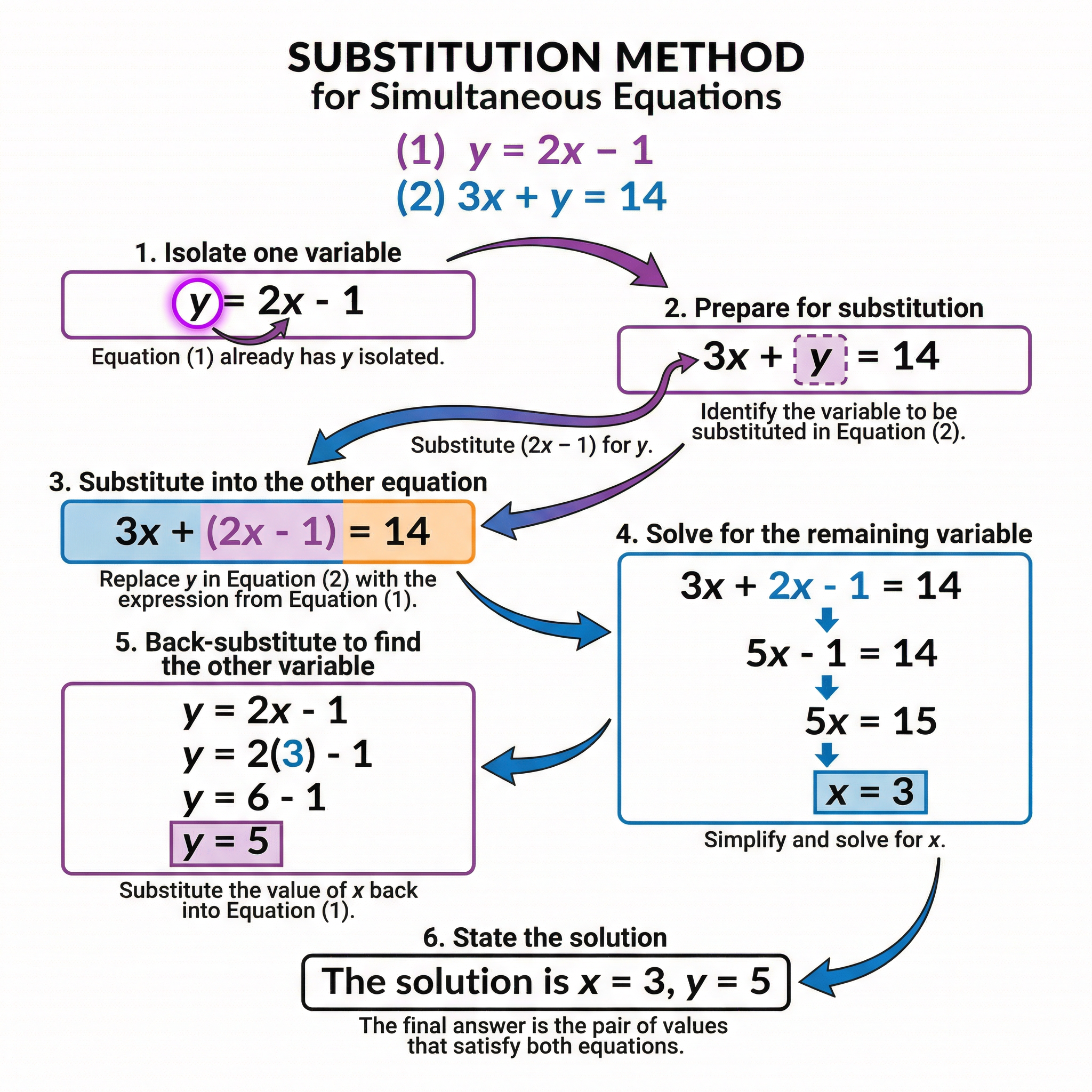
Concept 2: Solving by Substitution

The substitution method is another algebraic approach, which is particularly efficient when one of the equations is already written with one variable as the subject (e.g., y = ... or x = ...). The method involves substituting the expression for this variable into the second equation. This creates a new equation with only one variable, which can then be solved. As with the elimination method, the final step is to substitute the value of the first variable back into one of the original equations to find the second.

Example: Given the equations y = 2x - 1 and 3x + y = 14. The first equation gives an expression for y. We can substitute (2x - 1) into the second equation in place of y: 3x + (2x - 1) = 14. This simplifies to 5x - 1 = 14, then 5x = 15, so x = 3. Substituting x = 3 back into the first equation y = 2x - 1 gives y = 2(3) - 1, which results in y = 5.

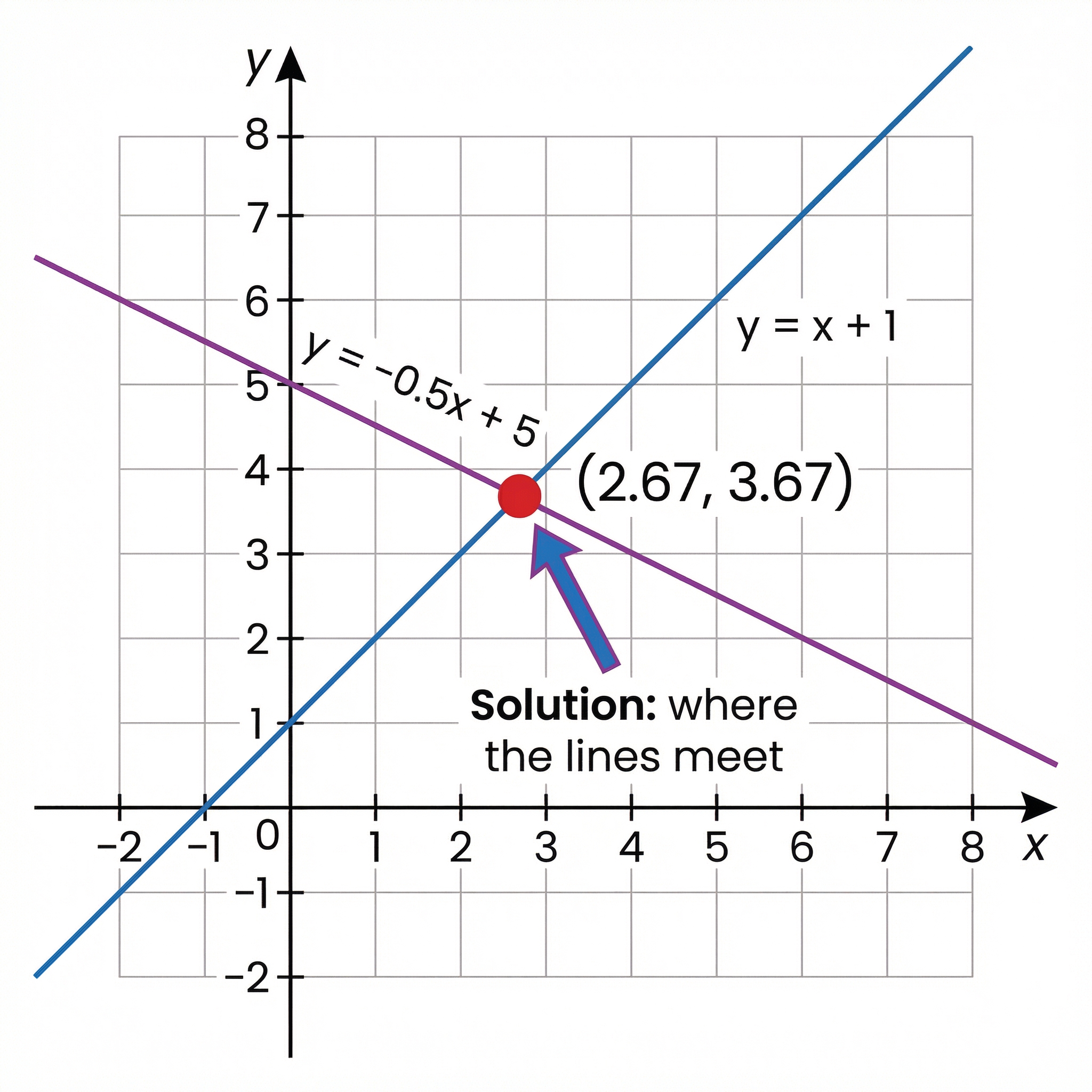
Concept 3: Graphical Interpretation

Every linear equation in two variables can be represented as a straight line on a Cartesian grid. When you have two simultaneous linear equations, you have two straight lines. The solution to the system is the point where these two lines intersect. The coordinates (x, y) of the intersection point are the unique values that satisfy both equations. While drawing graphs to find a solution is less common as a required method in non-calculator exams due to potential inaccuracies, understanding this graphical representation is vital. It provides a visual understanding of what it means to solve the system and is often tested in questions that provide a graph and ask for the solution to be read from it.

Example: To solve the equations y = x + 1 and y = -0.5x + 5 graphically, you would plot both lines. The point where they cross is the solution. By inspecting the graph, you can identify the coordinates of this intersection, which represents the x and y values that work for both equations.

Concept 4: Non-Linear Systems (Higher Tier Only)

Higher tier candidates must also be able to solve a system of two equations where one is linear and the other is quadratic. The substitution method is almost always the best approach here. The linear equation should be rearranged to make either x or y the subject. This expression is then substituted into the quadratic equation, resulting in a quadratic equation in one variable. This can be solved by factorising, using the quadratic formula, or completing the square. It is common for these systems to have two pairs of solutions, corresponding to two points of intersection between the line and the curve.

Example: Solve y = x + 1 and y = x^2 - 2x + 3. Substitute (x + 1) for y in the quadratic equation: x + 1 = x^2 - 2x + 3. Rearrange to form a quadratic set to zero: x^2 - 3x + 2 = 0. Factorising gives (x - 1)(x - 2) = 0, so x = 1 or x = 2. For each x value, find the corresponding y value using the linear equation: if x = 1, y = 1 + 1 = 2; if x = 2, y = 2 + 1 = 3. The solutions are (1, 2) and (2, 3).

Mathematical/Scientific Relationships

• General Form of a Linear Equation: ax + by = c
• Slope-Intercept Form: y = mx + c, where m is the gradient and c is the y-intercept. This form is useful for plotting graphs and for the substitution method.
• Quadratic Formula: For an equation ax^2 + bx + c = 0, the solutions for x are given by x = [-b ± sqrt(b^2 - 4ac)] / 2a. This is given on the formula sheet and is essential for solving non-linear systems when factorising is not possible.

Practical Applications

Simultaneous equations are used extensively in various fields to model and solve real-world problems. For example, in economics, they can be used to find the equilibrium point where supply equals demand. In business, they can help determine the break-even point where cost equals revenue. In physics and engineering, they are used to solve problems involving forces, circuits, and motion. A typical exam question might frame a problem in a real-world context, such as comparing two mobile phone tariffs or calculating the cost of different combinations of items.