Geometry and Measures Skills: Constructions

Overview

Geometric constructions are a fundamental part of the Geometry and Measures skills required for your Edexcel GCSE. This topic is all about precision and proof. It's not enough to simply draw a line that looks right; you must be able to create geometrically perfect lines, angles, and shapes using only a straight edge (ruler) and a pair of compasses. Examiners are specifically trained to look for your construction arcs as evidence of your method. Without them, you will lose marks, even if your final drawing is accurate. This skill is essential for both Foundation and Higher tiers, but at Higher level, it becomes the foundation for solving more complex problems involving loci. Mastering these constructions demonstrates a deep understanding of geometric properties and is a guaranteed way to pick up methodical marks in the exam.

Key Concepts

Concept 1: The Perpendicular Bisector

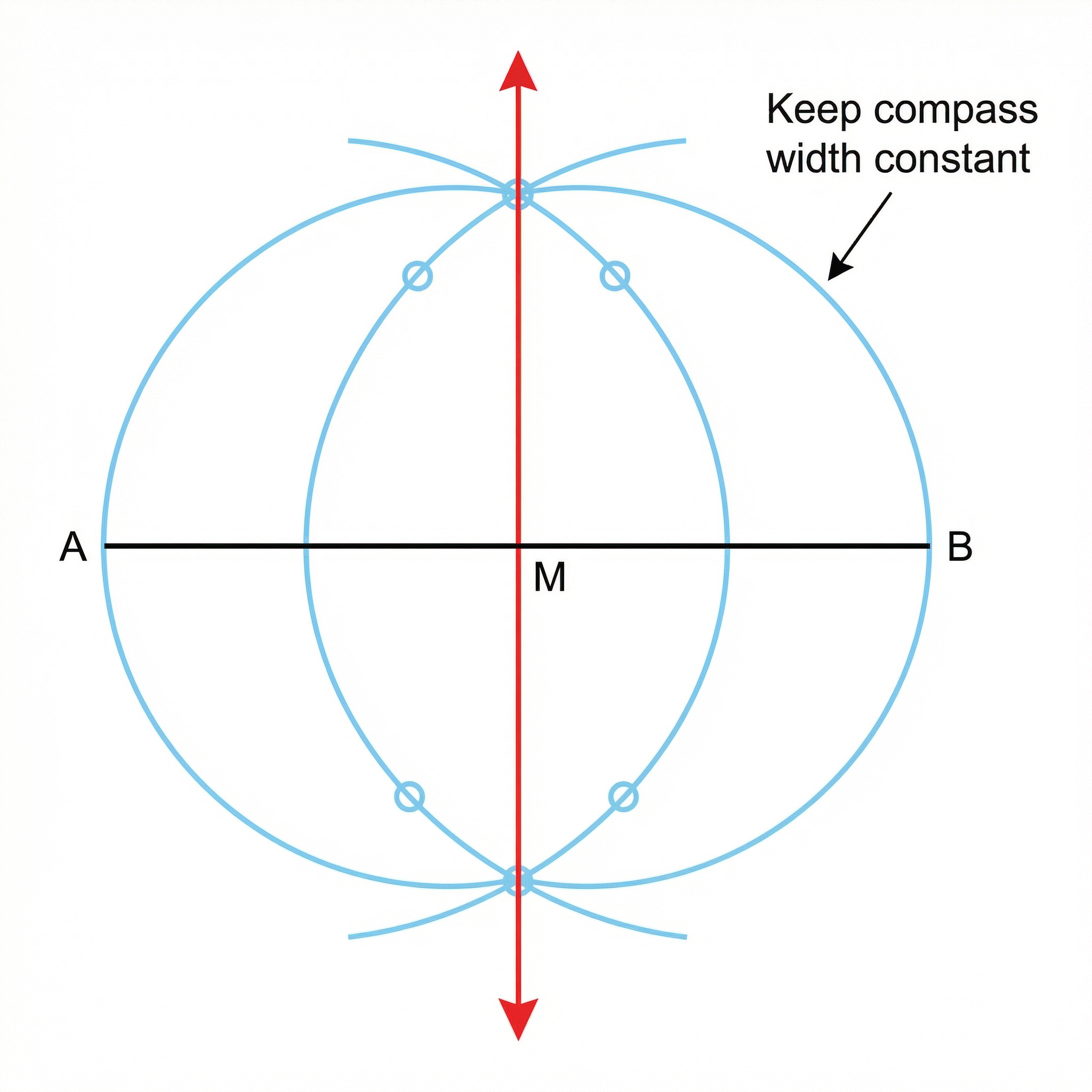
A perpendicular bisector is a line that cuts another line segment into two equal halves at a perfect 90-degree angle. Think of it as the ultimate line of symmetry for a segment. This construction is fundamental because it is also the locus of all points that are an equal distance (equidistant) from the two endpoints of the segment. So, if a question asks you to find points that are 'the same distance from A and B', your brain should immediately think: 'perpendicular bisector of the line AB'.

Method:

1. Start with a line segment, let's call it AB.
2. Open your compass to a width that is clearly more than half the length of AB. This is critical; if it's too short, your arcs won't intersect.
3. Place the compass point on A and draw a wide arc that goes both above and below the line segment.
4. Keeping the compass width exactly the same, move the compass point to B and draw another arc that intersects the first one in two places.
5. Use your ruler to draw a straight line connecting the two points where the arcs intersect. This new line is the perpendicular bisector.

Concept 2: The Angle Bisector

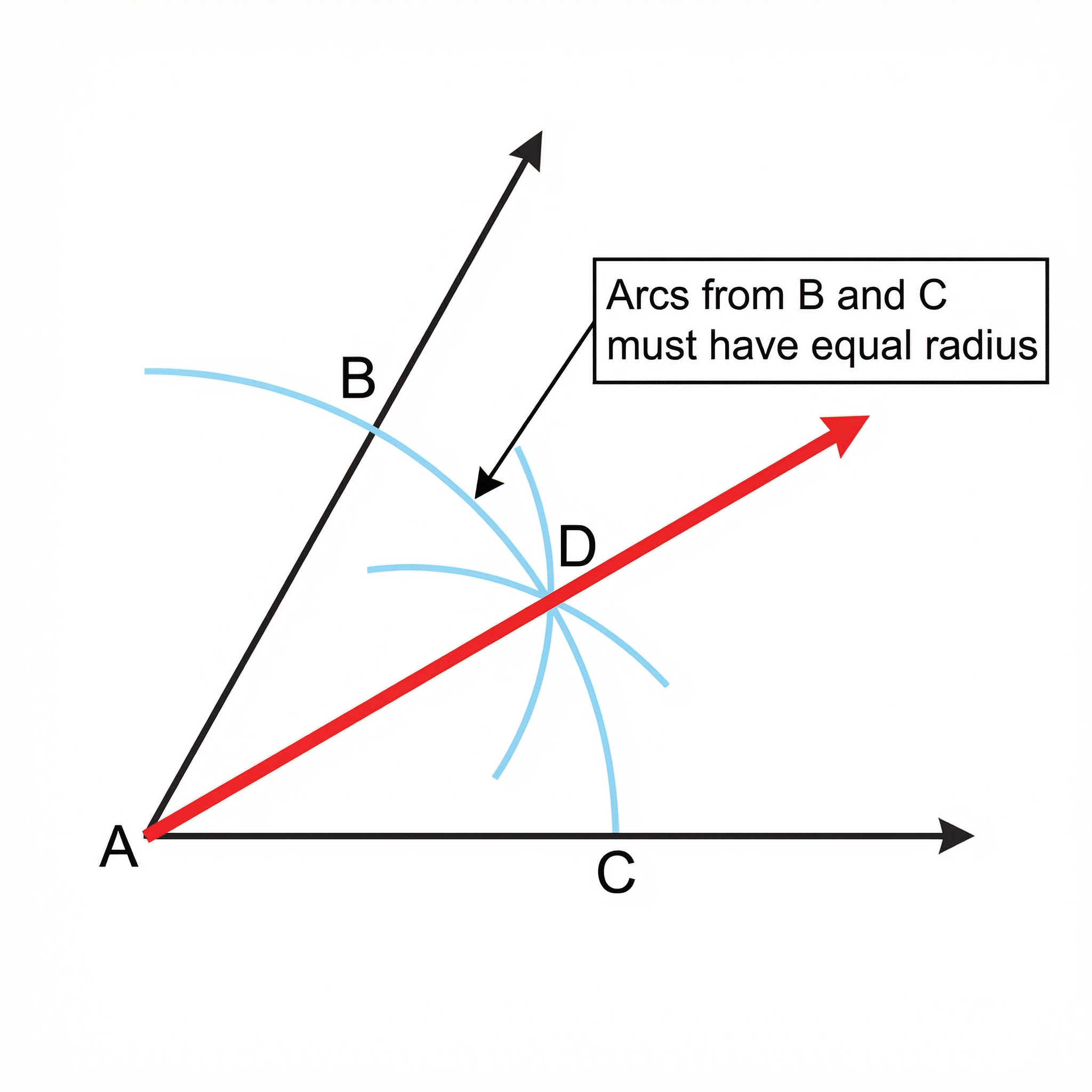
An angle bisector is a line or ray that divides an angle into two smaller, equal angles. Just like the perpendicular bisector, this is also a locus. The angle bisector is the locus of all points that are equidistant from the two lines that form the angle. So, if an exam question asks for the region that is 'closer to line X than line Y', you know you need to construct the bisector of the angle between them.

Method:

1. Start with an angle at vertex A.
2. Place your compass point on the vertex A and draw an arc that crosses both arms of the angle. Let's call these intersection points P and Q.
3. Place the compass point on P and draw an arc in the middle of the angle.
4. Keeping the compass width the same, move the compass point to Q and draw another arc that intersects the one you just made. Let's call this intersection point R.
5. Use your ruler to draw a straight line from the vertex A through the point R. This is your angle bisector.

Concept 3: Constructing Triangles (SSS, SAS, ASA)

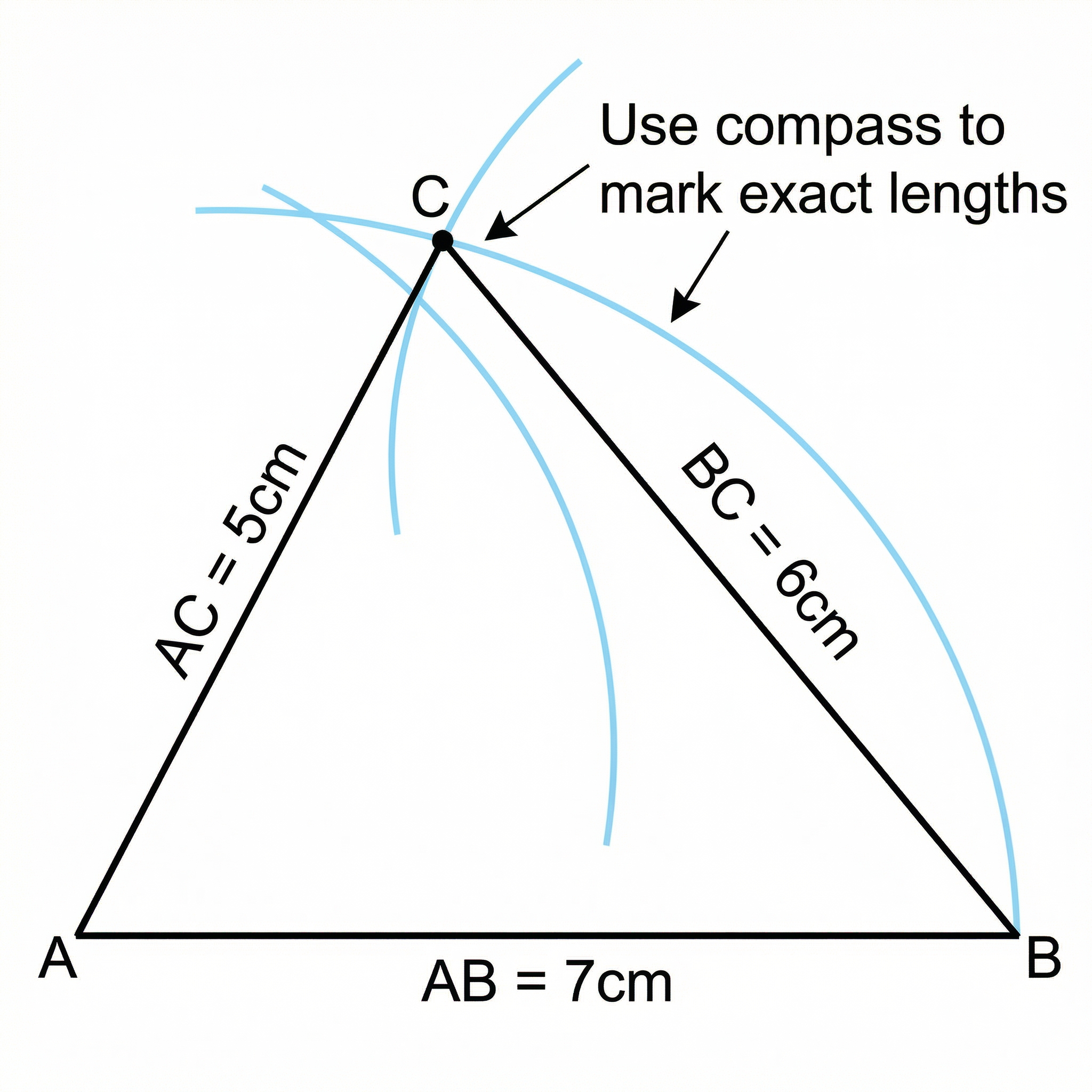
You can be asked to construct a triangle given specific information. The most common is SSS (Side-Side-Side), where you are given the lengths of all three sides.

Method (SSS):

1. Draw the longest side first using your ruler to get the exact length. Label the ends (e.g., A and B).
2. Set your compass to the length of the second side. Place the compass point on A and draw an arc.
3. Set your compass to the length of the third side. Place the compass point on B and draw a second arc that intersects the first one.
4. The point where the arcs cross is your third vertex, C. Connect A to C and B to C with your ruler to complete the triangle.

Mathematical/Scientific Relationships

There are no complex formulas to memorise for constructions, as it is a practical skill. However, the constructions themselves are based on fundamental geometric theorems:

• Perpendicular Bisector Theorem: Any point on the perpendicular bisector of a segment is equidistant from the endpoints of the segment.
• Angle Bisector Theorem: Any point on the bisector of an angle is equidistant from the two sides of the angle.

These theorems are the reason why constructions work and are the foundation for loci problems. You don't need to state the theorems, but understanding them helps you apply the correct construction.

Practical Applications

While constructions might seem abstract, they are the basis of design, architecture, and engineering. Think about designing a garden where a sprinkler needs to be placed equidistant from two trees (perpendicular bisector) or ensuring a security camera covers an equal angle on either side of a corner (angle bisector). Architects use these principles to create symmetrical and stable structures. In computer graphics and robotics, these geometric rules are programmed into algorithms to create paths and designs.