Study Notes

Overview
Loci and Constructions is a fascinating area of geometry that deals with the paths of points moving according to specific rules. For your Edexcel GCSE exam, this topic (specification point 3.11) is all about precision and method. You will be required to use a ruler and a pair of compasses to construct various loci, and crucially, to identify regions that satisfy multiple conditions at once. This skill is not just an abstract exercise; it forms the basis of many real-world applications, from GPS navigation to architectural design. In the exam, questions often appear in the context of maps or scale drawings, testing your ability to apply these pure mathematical skills to practical problems. A solid grasp of loci is vital as it connects directly to other areas of the specification, such as transformations, bearings, and inequalities, making it a cornerstone of geometric problem-solving.
Key Concepts
Concept 1: The Perpendicular Bisector
A perpendicular bisector is the locus of all points that are an equal distance (equidistant) from two fixed points. Imagine two towns, A and B. The line that represents all possible locations for a new supermarket that is exactly the same distance from both towns is the perpendicular bisector of the line segment AB. To construct it, you use a compass to create intersecting arcs from both points, ensuring your compass width is more than half the distance between them. The line joining the arc intersections is the perpendicular bisector. Examiners award marks for seeing your construction arcs, so never rub them out!
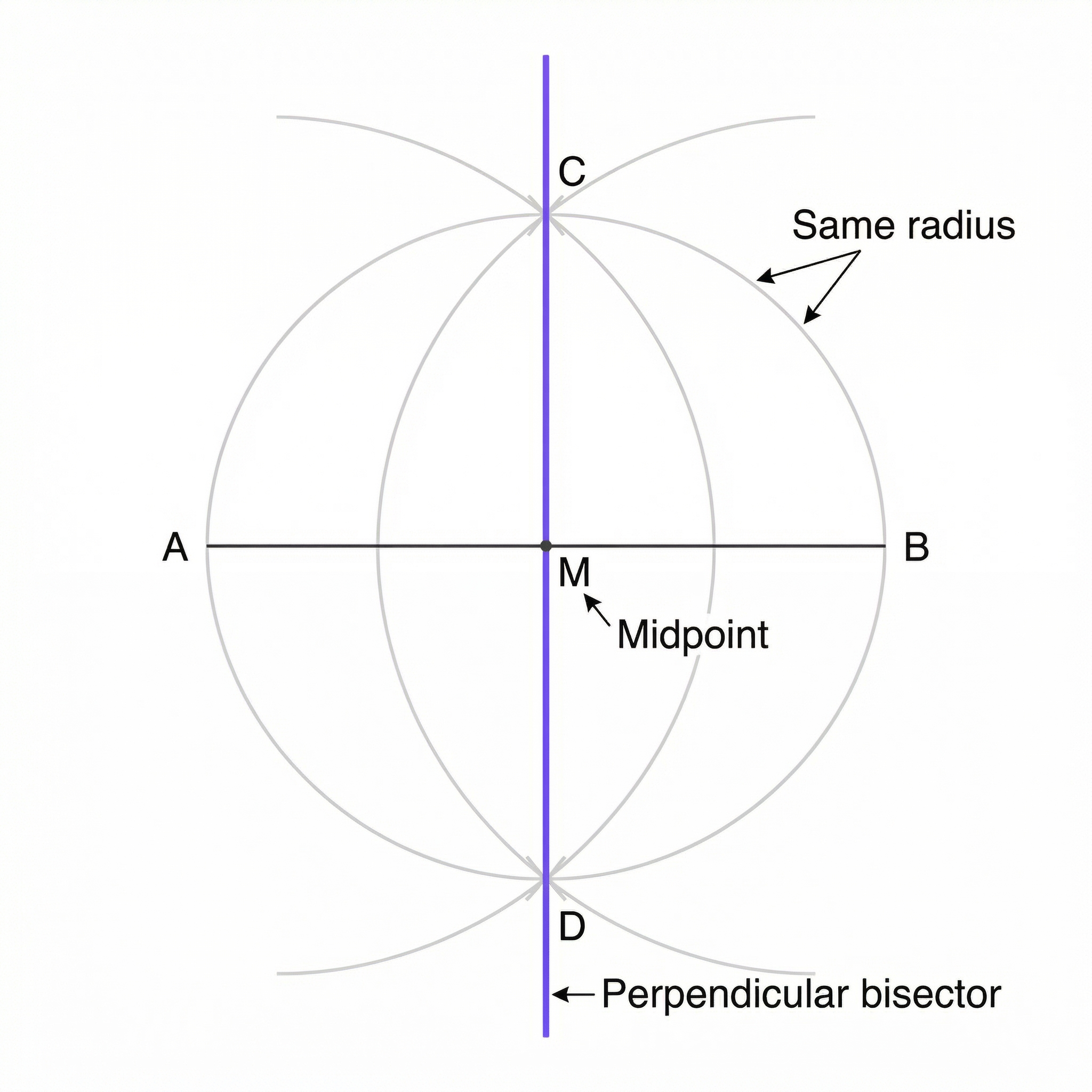
Example: If you have two points, P and Q, that are 8cm apart, the perpendicular bisector is the straight line where every point on it is equidistant from P and Q. It also cuts the line segment PQ exactly in half at a right angle.
Concept 2: The Angle Bisector
An angle bisector is the locus of all points that are equidistant from two intersecting lines. Think of it as a line that splits an angle perfectly in two. This is useful for finding a path that stays exactly in the middle of two boundaries, like a boat sailing down the centre of a channel. The construction involves creating an arc from the angle's vertex that crosses both lines, and then creating two further intersecting arcs from those crossing points. The line from the vertex through this final intersection is the angle bisector.
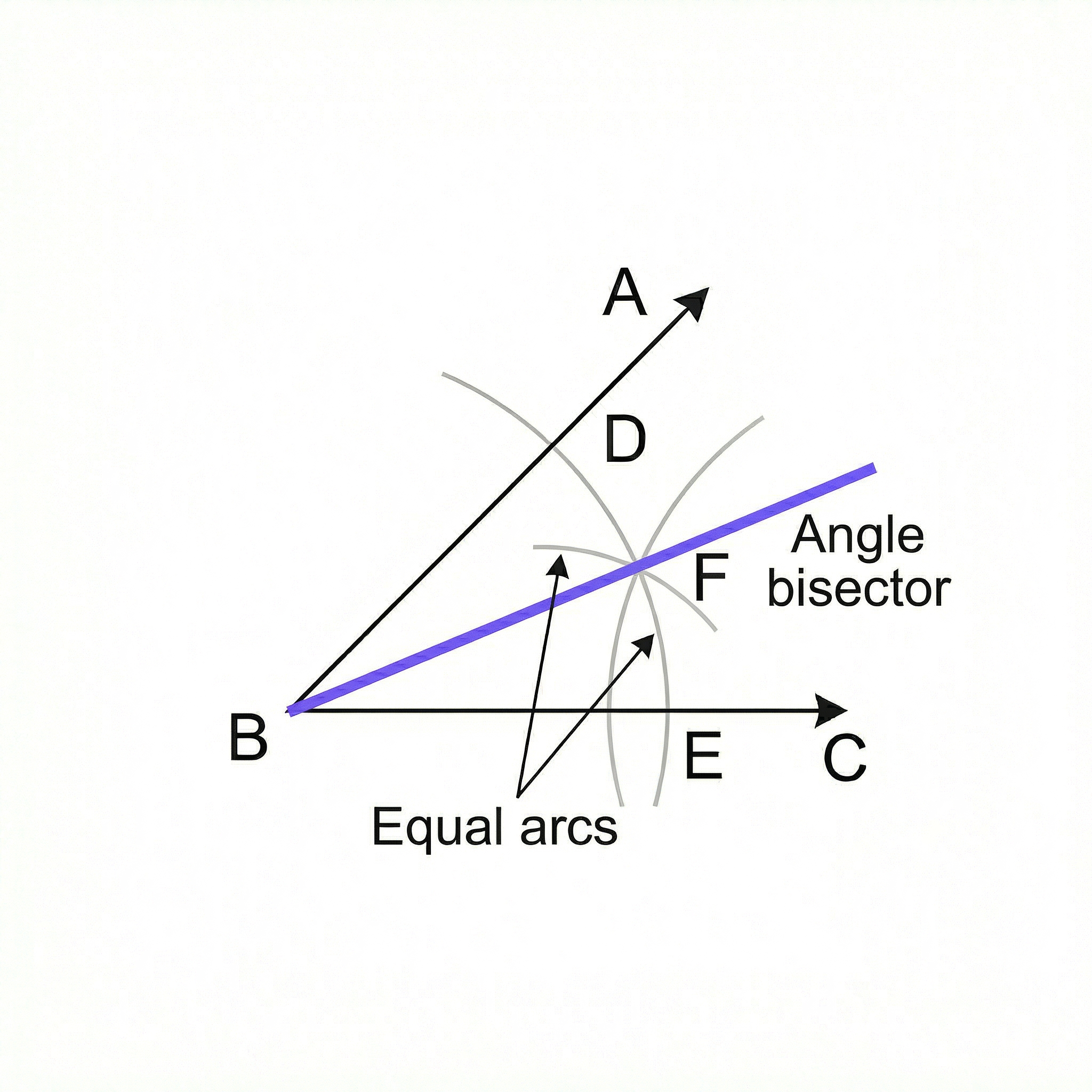
Example: Given an angle of 60 degrees, its bisector would create two smaller angles of exactly 30 degrees each.
Concept 3: Locus of Points a Fixed Distance from a Point
This is one of the most straightforward loci: the set of all points at a fixed distance from a single point. The shape this creates is always a circle. If a question asks for the locus of points 3cm from a point X, you simply set your compass to a radius of 3cm, place the point on X, and draw a full circle. This is often used in questions involving mobile phone masts or broadcast signals, where the signal reaches a certain circular radius.
Example: A goat is tethered to a post by a 5-metre rope. The area the goat can graze is a circle with a radius of 5 metres. The edge of this area is the locus of points exactly 5m from the post.
Concept 4: Locus of Points a Fixed Distance from a Line
This locus describes a path that is always the same distance from a given straight line. The result is a pair of parallel lines, one on each side of the original line. A common real-world analogy is the markings for a running track, where each lane must be a consistent distance from the lane next to it. For a line segment, the locus includes semi-circles at each end, creating a 'running track' shape.
Example: A dog runs in a field, always staying exactly 2 metres away from a long, straight fence. The path the dog can take is represented by two lines parallel to the fence, each 2 metres away from it.
Concept 5: Finding a Region (Higher Tier)
Higher tier candidates will be expected to combine these loci to identify a region that satisfies several conditions simultaneously. This is where the topic becomes a true test of problem-solving. You might be asked to shade the area that is 'closer to point A than to point B' AND 'less than 4cm from point C'. This requires you to construct a perpendicular bisector and a circle, and then use the inequalities ('closer to', 'less than') to identify the correct region to shade. A key tip is to use dashed lines for strict inequalities (e.g., < or >) and solid lines for inclusive inequalities (e.g., ≤ or ≥).
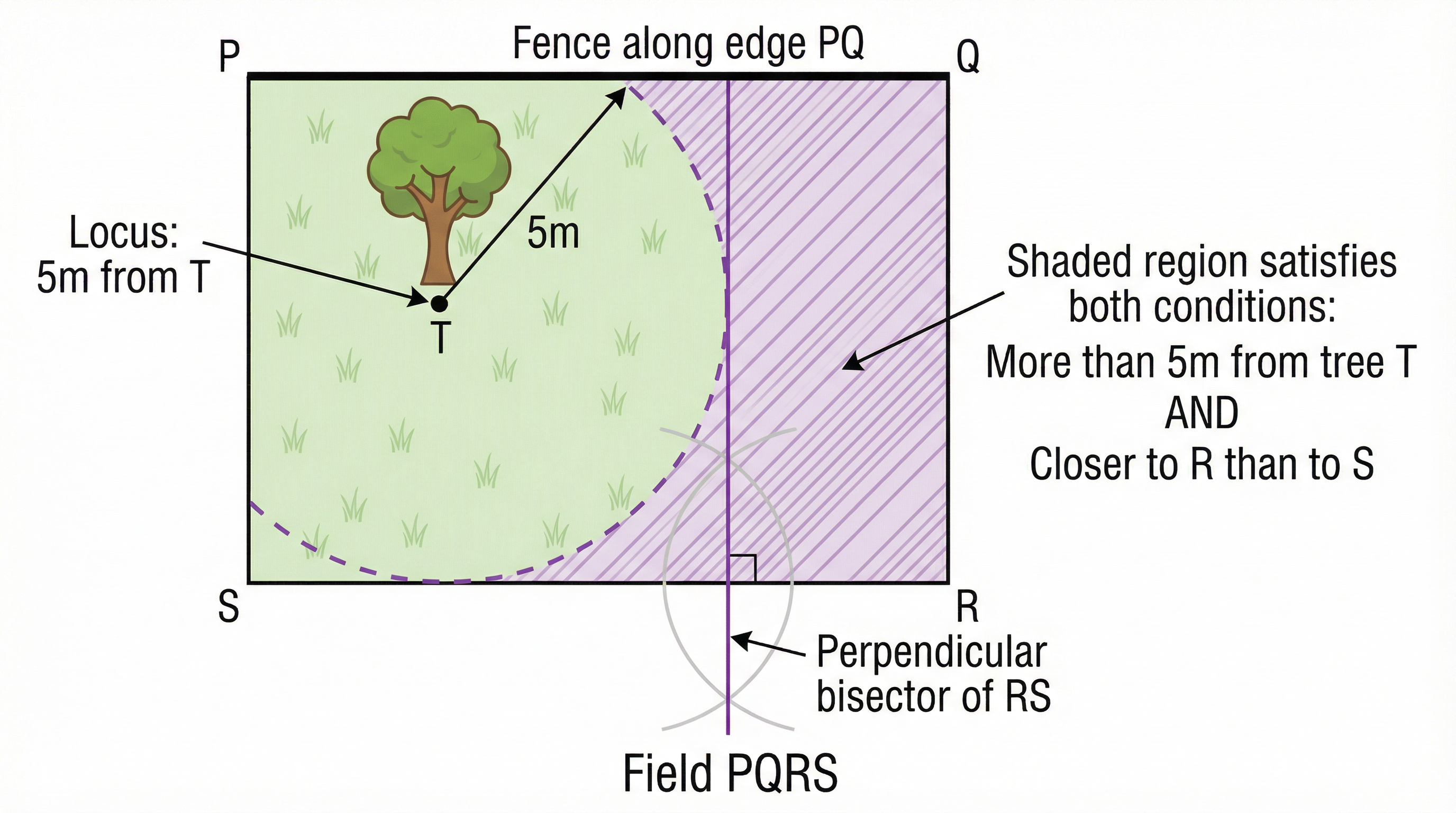
Mathematical/Scientific Relationships
There are no complex formulas to memorise for Loci, as it is a topic of geometric construction. The key relationships are the definitions themselves:
- Perpendicular Bisector: For any point P on the bisector of line segment AB, the relationship is PA = PB.
- Angle Bisector: For any point P on the bisector of angle ∠ABC, the perpendicular distance from P to line AB is equal to the perpendicular distance from P to line BC.
- Circle: For any point P on a circle with centre C and radius r, the relationship is PC = r.
These relationships are fundamental and are tested through your ability to construct them accurately.
Practical Applications
Loci are used everywhere in the real world:
- GPS and Navigation: Your phone's GPS uses signals from multiple satellites. The locus of points equidistant from two satellites is a plane, and the intersection of these planes pinpoints your location.
- Architecture and Town Planning: Architects use loci to determine where to place structures, ensuring they meet regulations like being a certain distance from a boundary or another building.
- Mobile Phone Networks: The area covered by a mobile phone mast is a circular locus. Network planners use this to ensure there are no gaps in coverage.
- Robotics: A robot arm's reach can be described by loci, defining the workspace it can operate within.
