Study Notes
Overview
Probability at A-Level is the mathematical study of uncertainty, but for your OCR exam, it is much more than simply rolling dice. It is a rigorous application of logic and notation that forms the bedrock of statistics and data modelling. Examiners are looking for candidates who can translate complex, wordy scenarios into precise mathematical statements, manipulate formulae with accuracy, and interpret their results in context. This topic frequently connects with other areas of the specification, such as data analysis and hypothesis testing, making it a cornerstone of the A-Level course. Typical exam questions involve Venn diagrams, tree diagrams, and formal proofs of independence, often requiring you to deconstruct a problem piece by piece to earn full marks.
Key Concepts
1. Set Notation and Venn Diagrams
At the heart of probability is the language of sets. You must be fluent in the use of union (∪, meaning 'A or B or both'), intersection (∩, meaning 'A and B'), and complement (', meaning 'not A'). A Venn diagram is your most powerful tool for visualizing these relationships. It allows you to map out the entire sample space and the relationships between different events, making complex calculations more intuitive.

Examiner Tip: Always draw a Venn diagram for questions involving overlapping categories. Credit is often given for a correctly labelled diagram where all probabilities sum to 1.
2. The Addition Rule
The General Addition Rule is a fundamental formula that you must be able to state and apply. It allows you to find the probability of the union of two events.
Formula: P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
We subtract the intersection P(A ∩ B) because it is counted twice when we add P(A) and P(B) together. Forgetting this is a very common error that examiners see every year.
3. Conditional Probability
This is one of the most challenging but important concepts. Conditional probability deals with situations where the probability of an event is dependent on the outcome of a previous event. The key phrase to look for is 'given that'. This signals a restriction of the sample space.
Formula: P(A|B) = P(A ∩ B) / P(B)
This reads as 'the probability of A given that B has occurred'. The denominator is the probability of the condition, P(B), not the total probability. A tree diagram is an excellent way to visualize conditional probabilities in multi-stage experiments.
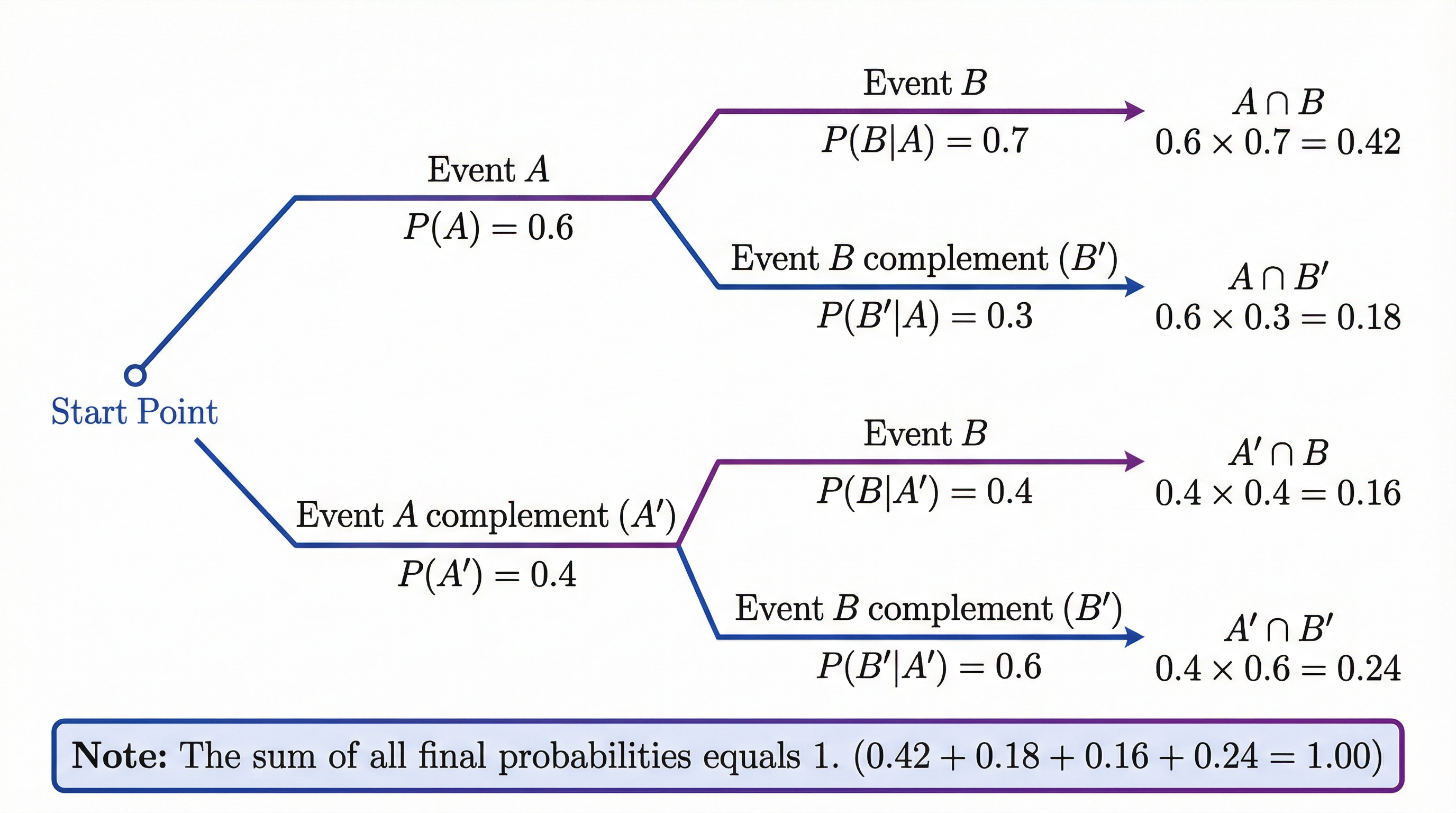
4. Independence
Two events are independent if the occurrence of one does not affect the probability of the other. For example, flipping a coin twice. To prove independence, you must use the multiplication rule.
Test for Independence: Events A and B are independent if and only if P(A ∩ B) = P(A) × P(B).
Examiner Tip: When a question asks you to 'Show that' two events are independent, you must perform this calculation explicitly and make a concluding statement. Simply stating they are independent is not enough to earn the marks.
Mathematical/Scientific Relationships
- General Addition Rule: P(A ∪ B) = P(A) + P(B) - P(A ∩ B) (Given on formula sheet)
- Conditional Probability: P(A|B) = P(A ∩ B) / P(B) (Must memorise)
- Independence Test: Events A and B are independent if P(A ∩ B) = P(A) × P(B) (Must memorise)
- Complement Rule: P(A') = 1 - P(A) (Must memorise)
- For Mutually Exclusive Events: P(A ∩ B) = 0 and P(A ∪ B) = P(A) + P(B) (Must memorise)
Practical Applications
Probability is not just an abstract concept; it is used everywhere in the real world. It is the foundation of the insurance industry, where actuaries calculate risks to determine premiums. In medicine, it is used to assess the effectiveness of new drugs and treatments in clinical trials. In finance, it is used to model the behavior of stock markets and manage investment risk. Understanding probability allows you to make informed decisions in the face of uncertainty, a skill that is valuable in any field.