Ratio and proportion

Overview

Ratio and Proportion (OCR Topic 1.4) is a fundamental concept in mathematics that bridges the gap between arithmetic and algebra. It's not just about dividing numbers; it's about understanding the multiplicative relationships between quantities. Examiners value this topic because it tests your ability to reason logically and apply mathematical principles to real-world scenarios. From scaling recipes and converting currencies to interpreting maps and analyzing scientific data, ratios are everywhere. In your exam, you can expect to see questions ranging from simple ratio simplification to complex multi-step problems involving algebraic ratios and inverse proportion, making a solid understanding essential for both Foundation and Higher tier candidates.

Key Concepts

Concept 1: Simplifying Ratios

A ratio is a way of comparing the relative sizes of two or more quantities. The most crucial first step, and one where many candidates lose marks, is ensuring all parts of the ratio are in the same units. You cannot compare 50cm to 2m directly. You must convert them to a common unit, like centimeters, giving you a ratio of 50:200. Once the units are consistent, you simplify the ratio by finding the highest common factor (HCF) of all parts and dividing each part by it. For 50:200, the HCF is 50. Dividing both parts by 50 gives the simplified ratio 1:4. This process ensures the relationship is expressed in its most basic, easy-to-understand form.

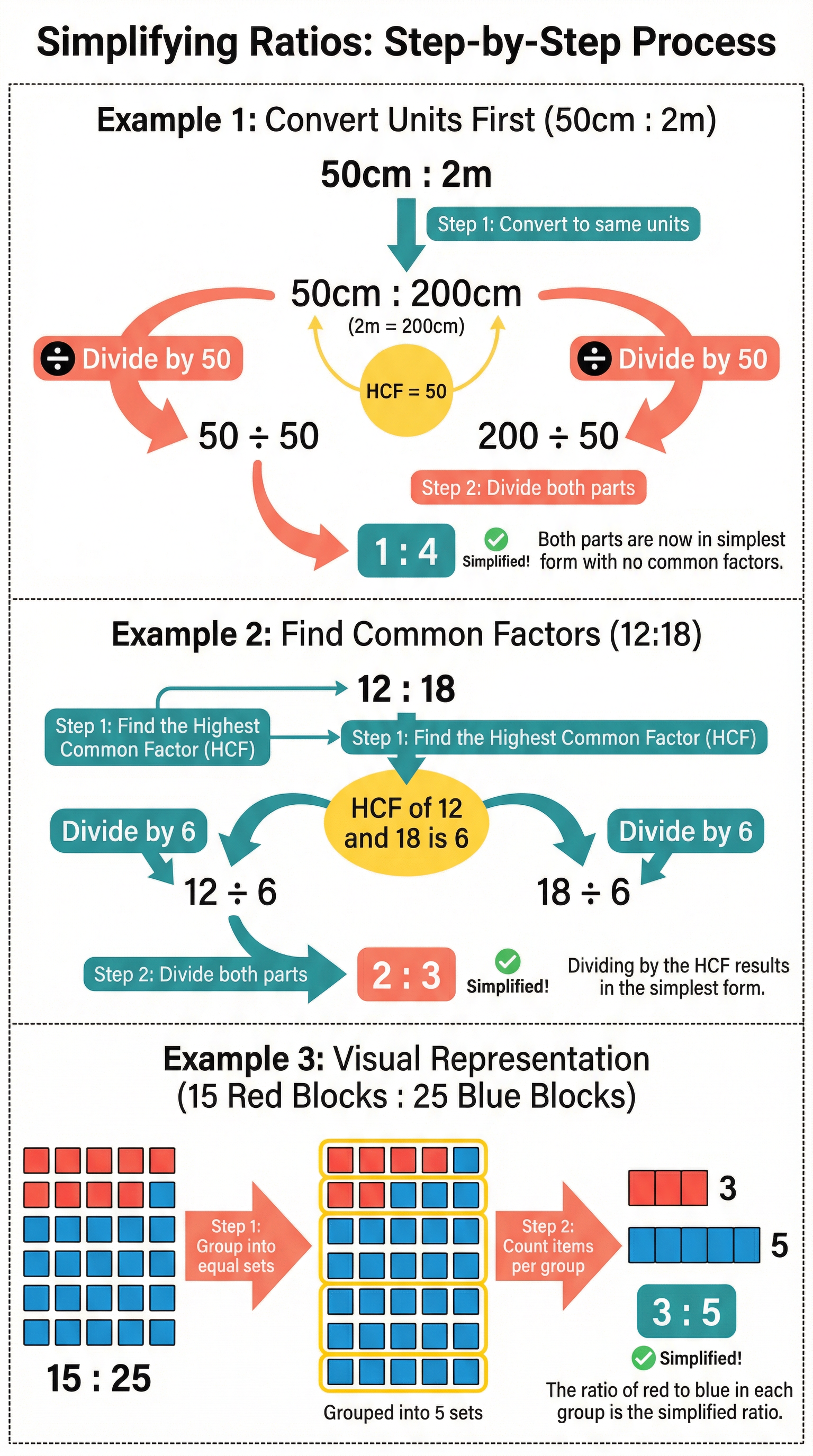
Example: Simplify the ratio 90p : £3.00

1. Convert to common units: £3.00 is 300p.
2. Write the ratio: 90 : 300
3. Find the HCF: The HCF of 90 and 300 is 30.
4. Divide by HCF: 90 ÷ 30 = 3; 300 ÷ 30 = 10.
5. Simplified Ratio: 3:10

Concept 2: Dividing a Quantity in a Given Ratio

This is a classic exam question style. When asked to divide an amount into a ratio, you are splitting it into a set number of parts. The key is to find the value of one single part first (the unitary method). To do this, you add the numbers in the ratio to find the total number of parts. Then, divide the total quantity by this sum. Finally, multiply the value of one part by each number in the ratio to find the size of each share.

Example: Share £56 in the ratio 3:5.

1. Find total parts: 3 + 5 = 8 parts.
2. Find value of one part: £56 ÷ 8 = £7 per part.
3. Calculate shares:
   • 3 parts = 3 × £7 = £21
   • 5 parts = 5 × £7 = £35
4. Check: £21 + £35 = £56. The calculation is correct.

Concept 3: Direct and Inverse Proportion

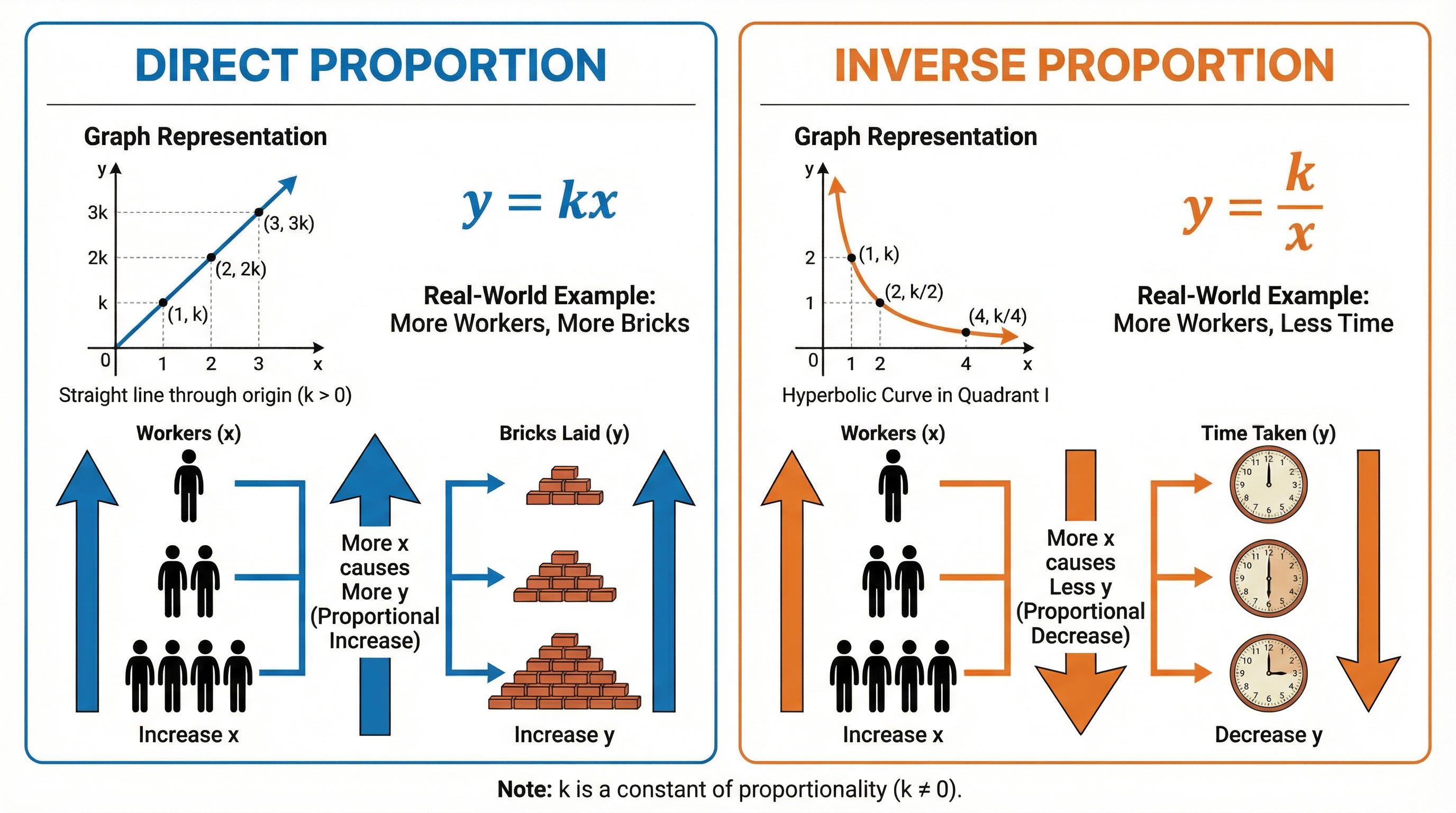
Proportion describes how two quantities are related. Examiners will test both direct and inverse proportion.

• Direct Proportion: As one quantity increases, the other increases at the same rate. The graph is a straight line through the origin, and the formula is y = kx, where 'k' is the constant of proportionality. Think of buying items: the more you buy, the more it costs.
• Inverse Proportion: As one quantity increases, the other decreases proportionally. The graph is a hyperbola, and the formula is y = k/x. Think of speed and time: the faster you travel, the less time the journey takes.

For Higher tier candidates, this can extend to non-linear relationships, such as y being proportional to the square of x (y = kx²) or inversely proportional to the square root of x (y = k/√x).

Mathematical/Scientific Relationships

• Ratio Simplification: To simplify a:b, find HCF(a,b) and divide both a and b by it.
• Unitary Method: Find the value of one part, then multiply to find the value of the required number of parts.
• Direct Proportion Formula: y = kx (Must memorise)
• Inverse Proportion Formula: y = k/x (Must memorise)
• Finding the Constant (k): Rearrange the formula and substitute a known pair of values. For direct, k = y/x. For inverse, k = yx.

Practical Applications

• Recipes: Scaling ingredients up or down. If a recipe for 4 people needs 200g of flour, how much is needed for 6? This is a direct proportion problem.
• Maps: The scale on a map (e.g., 1:50000) is a ratio. It tells you that 1cm on the map represents 50000cm (or 500m) in real life.
• Currency Exchange: Exchange rates are ratios between different currencies (e.g., £1 : $1.25).
• Best Buy Problems: Comparing products to find which offers better value for money involves calculating and comparing unit prices—a practical application of the unitary method.

'