Study Notes
Overview
Coordinate Geometry is a cornerstone of the WJEC GCSE Mathematics syllabus, forming a bridge between algebra and geometry. At its heart, this topic is about the relationship between equations and the straight lines they represent on a Cartesian grid. For your exam, a deep understanding of the equation y = mx + c is non-negotiable; it is the key that unlocks the majority of marks. Examiners frequently test your ability to manipulate linear equations, calculate gradients (the steepness of a line), and identify y-intercepts (where a line crosses the y-axis). This topic connects directly to graphical representation of data, algebraic rearrangement, and even trigonometry in more advanced contexts. Typical exam questions range from simple identification of features from a graph to multi-step problems requiring you to find the equation of a line that is parallel or perpendicular to another. Mastering these skills is essential, as they provide a reliable foundation for scoring well in both calculator and non-calculator papers.
Key Concepts
Concept 1: The Equation of a Straight Line: y = mx + c
This is the single most important formula in coordinate geometry. It defines every straight line on a 2D plane.
- y: Represents the vertical coordinate of any point on the line.
- x: Represents the horizontal coordinate of any point on the line.
- m: Represents the gradient of the line. It tells us how steep the line is. A positive gradient means the line slopes upwards from left to right. A negative gradient means it slopes downwards. A gradient of 0 means the line is horizontal.
- c: Represents the y-intercept. This is the point where the line crosses the vertical y-axis. Its coordinate is always (0, c).
Why it works: This equation is a rule that connects the x and y coordinates for every single point that lies on the line. For any given x-value, multiplying it by the gradient 'm' and adding the intercept 'c' will give you the exact corresponding y-value on that line.
Example: Consider the equation y = 2x + 1. The gradient (m) is 2, and the y-intercept (c) is 1. This means the line crosses the y-axis at (0, 1). For every 1 unit you move to the right along the x-axis, the line rises by 2 units vertically.
Concept 2: Calculating the Gradient (m)
The gradient measures the steepness of a line and is calculated as the 'change in y' divided by the 'change in x'.
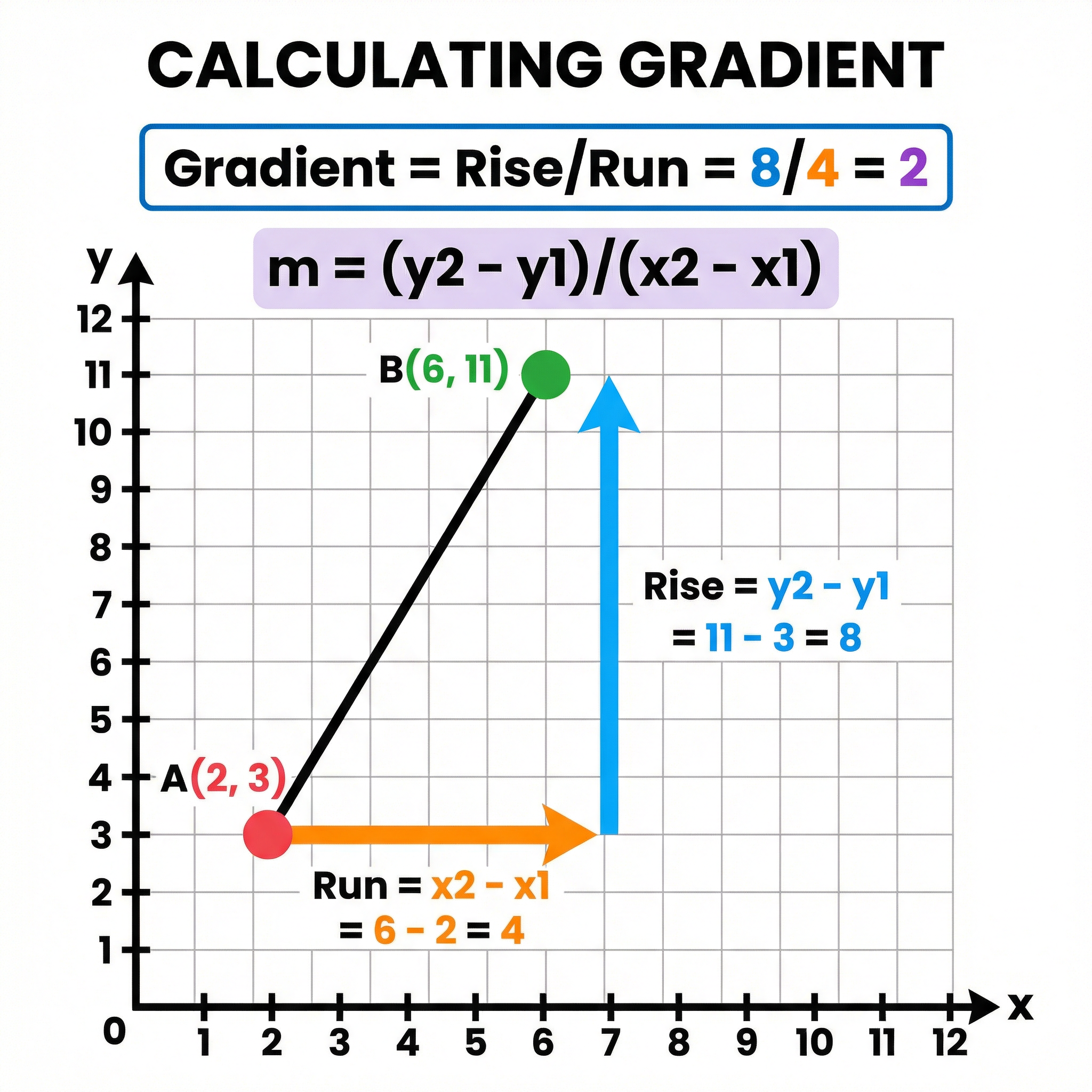
Formula: Given two points (x₁, y₁) and (x₂, y₂), the gradient 'm' is:
m = (y₂ - y₁) / (x₂ - x₁) (Must memorise)
This is often remembered as Rise over Run. The 'Rise' is the vertical change, and the 'Run' is the horizontal change.
Example: Find the gradient of the line connecting points A(2, 3) and B(4, 9).
- Let A be (x₁, y₁) and B be (x₂, y₂).
- Rise = y₂ - y₁ = 9 - 3 = 6
- Run = x₂ - x₁ = 4 - 2 = 2
- Gradient m = Rise / Run = 6 / 2 = 3
Credit is given for correct substitution into the formula, even if the final calculation is incorrect.
Concept 3: Parallel and Perpendicular Lines
Parallel Lines: Two lines are parallel if they have the exact same gradient. They will never intersect.
- If line L₁ has equation y = 3x + 2, and line L₂ is parallel to it, then the gradient of L₂ is also 3.
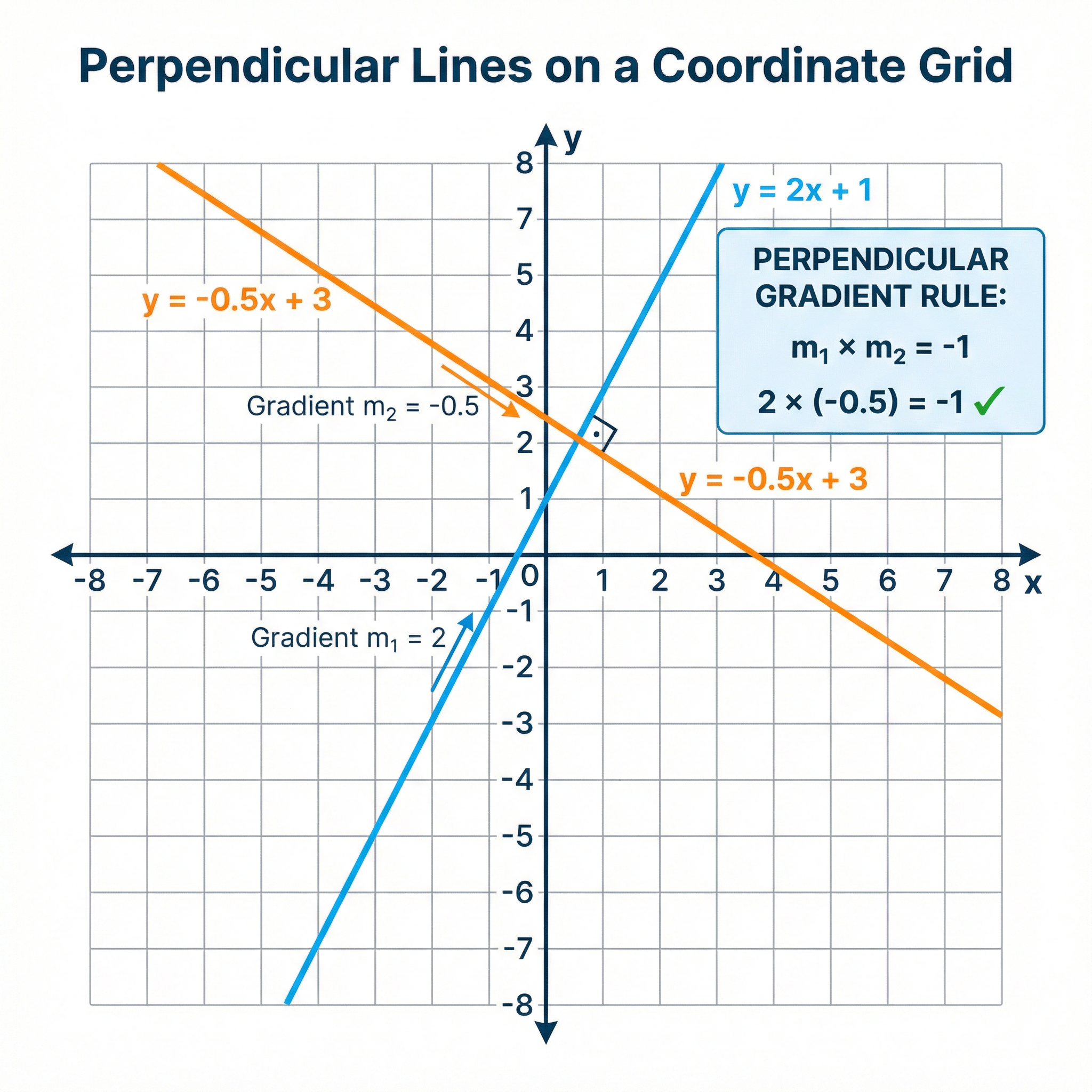
Perpendicular Lines (Higher Tier): Two lines are perpendicular if they intersect at a right angle (90°). The rule is that the product of their gradients is -1.
- m₁ × m₂ = -1 (Must memorise)
Example: A line L₁ has a gradient of 2. A line L₂ is perpendicular to L₁.
- To find the gradient of L₂, we use the rule: 2 × m₂ = -1
- Therefore, m₂ = -1/2.
- A quick way to find the perpendicular gradient is to find the negative reciprocal: flip the fraction and change the sign. The gradient 2 is the same as 2/1. Flipping it gives 1/2, and changing the sign gives -1/2.
Mathematical Relationships
- Equation of a Line: y = mx + c (Must memorise)
- Gradient Formula: m = (y₂ - y₁) / (x₂ - x₁) (Must memorise)
- Parallel Lines: m₁ = m₂ (Must memorise)
- Perpendicular Lines (Higher Tier): m₁ × m₂ = -1 (Must memorise)
- Midpoint of a Line Segment (Higher Tier): ((x₁ + x₂)/2, (y₁ + y₂)/2) (Given on formula sheet)
- Length of a Line Segment (Higher Tier): √((x₂ - x₁)² + (y₂ - y₁)²). This is an application of Pythagoras' theorem. (Given on formula sheet)
Practical Applications
Coordinate geometry is used extensively in the real world:
- Computer Graphics: Video games and animations use coordinate systems to position characters and objects on screen.
- Navigation: GPS systems use coordinates (latitude and longitude) to pinpoint locations and calculate routes.
- Engineering and Architecture: Blueprints for buildings and bridges rely on coordinate geometry to specify the precise location of every component.
- Business Analytics: Companies plot sales data on graphs to identify trends (gradients) and starting points (y-intercepts).
