Study Notes

Overview
Welcome to the essential guide for mastering Evaluating Methods (4.4) for your Edexcel GCSE Combined Science exam. This topic is not just another section to memorise; it is a fundamental scientific skill that examiners love to test. A significant portion of your final grade, particularly the 60% of marks from Assessment Objective 3 (AO3), depends on your ability to analyse, interpret, and evaluate experimental procedures. In this guide, we will dissect the core concepts of validity, accuracy, and precision, explore the different types of experimental errors, and equip you with the techniques to suggest and justify improvements to a given method. By understanding how to think like an examiner and critique a practical, you can turn challenging 6-mark questions into a reliable source of marks across all your science papers.
Key Concepts
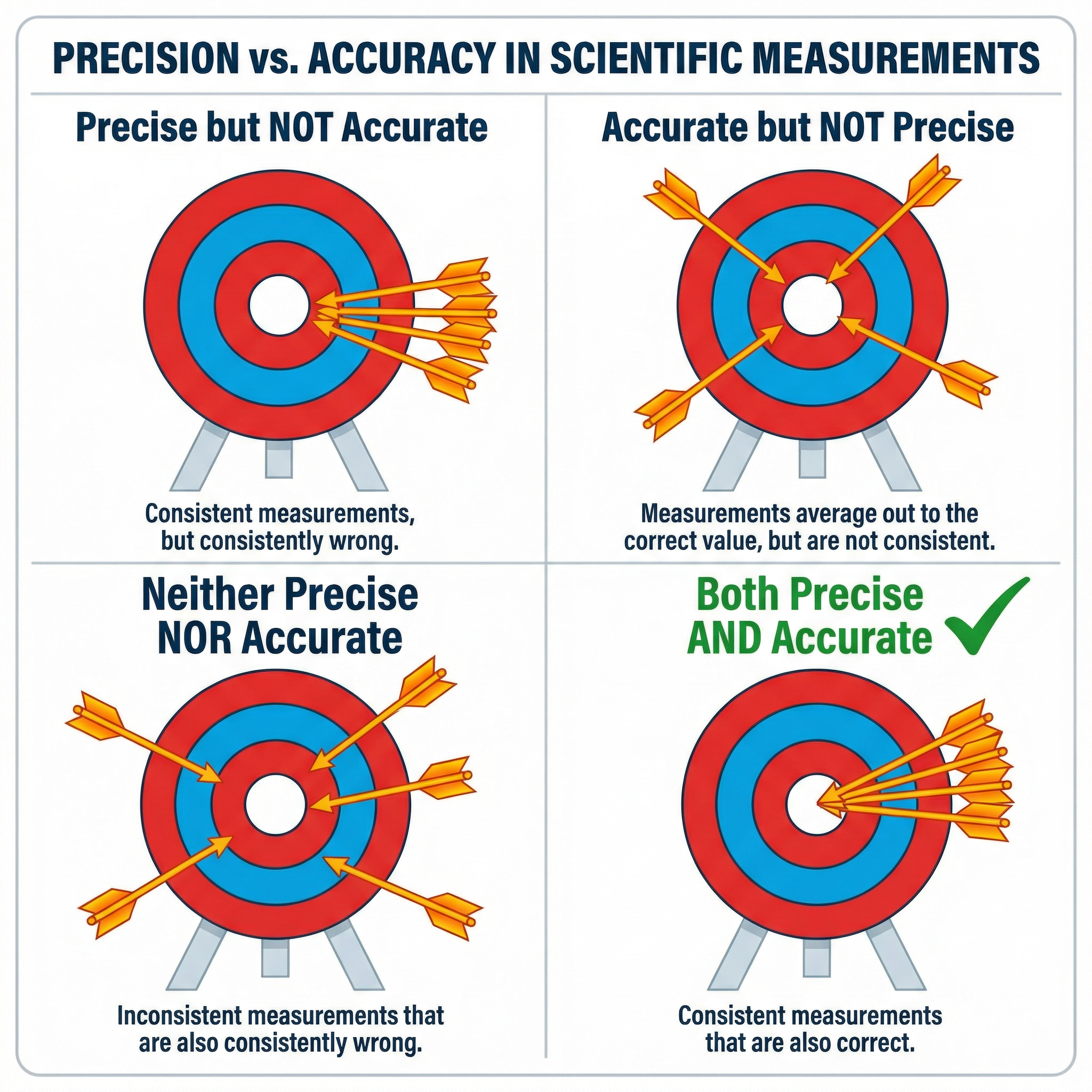
Concept 1: Validity, Accuracy, and Precision
These three terms are the bedrock of experimental evaluation, but they are frequently confused by candidates. To secure marks, you must use them correctly.
-
Validity: An experiment is valid if it is a fair test of its aim. This means you are only changing the independent variable and measuring the dependent variable, while keeping all other potential variables constant. These are called control variables. If a control variable is not kept constant, it could affect the results, making the experiment invalid. For example, when testing the effect of light intensity on the rate of photosynthesis, if the temperature also changes, you cannot be sure whether it was the light or the temperature that caused the change in results. Credit is given for identifying a specific uncontrolled variable that impacts the outcome.
-
Accuracy: This refers to how close a measurement is to the true value. For example, if the true boiling point of a substance is 78.5°C and your measurement is 78.4°C, your result is highly accurate. Accuracy is often compromised by systematic errors.
-
Precision: This describes the closeness of repeated measurements to each other. If you measure the length of an object five times and get 15.2cm, 15.1cm, 15.2cm, 15.2cm, and 15.1cm, your measurements are very precise. However, they might not be accurate if the ruler you used had a zero error. Precision is affected by random errors.
Concept 2: Types of Experimental Error
Examiners expect you to identify specific errors in a method, not just vaguely state 'human error'. All experimental errors fall into two categories.
-
Random Errors: These are unpredictable variations in measurements that cause readings to be scattered around the true value. They affect the precision of your results. Examples include fluctuations in room temperature, misreading a scale, or variations in your reaction time when using a stopwatch. The effect of random errors can be reduced by taking multiple readings and calculating a mean. This helps to cancel out the random highs and lows.
-
Systematic Errors: These are consistent errors that cause every measurement to be shifted in the same direction away from the true value. They affect the accuracy of your results. Examples include a thermometer that consistently reads 2°C too high (a calibration error), reading a volume from the top of the meniscus instead of the bottom (a procedural error), or heat loss to the surroundings in an exothermic reaction practical. Repeating the experiment will not remove systematic errors; you must identify the source of the error and correct the procedure or calibrate the apparatus.

Concept 3: Improving Methods
This is where you can earn significant marks. When asked to improve a method, you must use the 'Change + Reason' structure. State a specific change and then justify how it improves the quality of the data (i.e., improves validity, accuracy, or precision).
Example: Instead of just saying 'use a data logger', a high-credit answer would be: 'Replace the manual stopwatch with a computer-based data logger and light gates (Change). This eliminates human reaction time error (Reason), thereby increasing the accuracy of the time measurements.'
Common improvements include:
- Using a gas syringe instead of counting bubbles to measure gas volume more accurately.
- Using a digital thermometer for higher resolution and to avoid parallax error.
- Using a water bath to maintain a constant temperature.
- Insulating a beaker to reduce heat loss to the surroundings.
Mathematical/Scientific Relationships
Calculating the Mean
When you have a set of repeat readings, you should calculate the mean to get a more reliable estimate of the true value. However, you must first identify and discard any anomalies (results that do not fit the pattern).
Formula: Mean = Sum of all readings / Number of readings
Example: A student measures the time taken for a reaction at 40°C three times and gets the following results: 25.2 s, 25.4 s, 29.1 s.
- Identify the anomaly: 29.1 s is clearly an anomaly as it is not close to the other two readings.
- Discard the anomaly.
- Calculate the mean of the remaining results: (25.2 + 25.4) / 2 = 25.3 s.
Uncertainty
Every measurement has an uncertainty, which is usually half the range of the repeated readings, or half the resolution of the measuring instrument.
Formula: Uncertainty = Range / 2 = (Highest reading - Lowest reading) / 2
Example: Using the concordant results from above (25.2 s and 25.4 s):
- Range = 25.4 - 25.2 = 0.2 s
- Uncertainty = 0.2 / 2 = ±0.1 s
- The final result is written as 25.3 s ± 0.1 s.
Practical Applications
These evaluation skills are essential for all your Core Practicals. For example, in the 'Investigating the effect of concentration on reaction rate' practical, you might be asked to evaluate the method of measuring the 'disappearing cross'.
- Critique: The main weakness is that judging the point at which the cross disappears is subjective and varies between observers. This introduces a random error.
- Improvement: Use a light sensor and a data logger placed under the flask. Start a timer and record the light level. Stop the timer when the light level drops to a specific, pre-determined value. This removes the subjective judgement and human reaction time error, making the results more precise and accurate.