Waves

Overview

Waves are a fundamental concept in physics, describing how energy is transferred through space and matter. This topic explores the essential properties of waves, their mathematical relationships, and their diverse applications, from communication to medical imaging. A solid understanding of waves is crucial for success in your GCSE Combined Science exam, as it forms the basis for many other areas of physics, including light, sound, and electromagnetism. Examiners frequently test candidates on their ability to apply the wave equation, interpret wavefront diagrams, and recall the properties and uses of the electromagnetic spectrum. This guide will equip you with the knowledge and skills to tackle these questions with confidence.

Key Concepts

Concept 1: Transverse and Longitudinal Waves

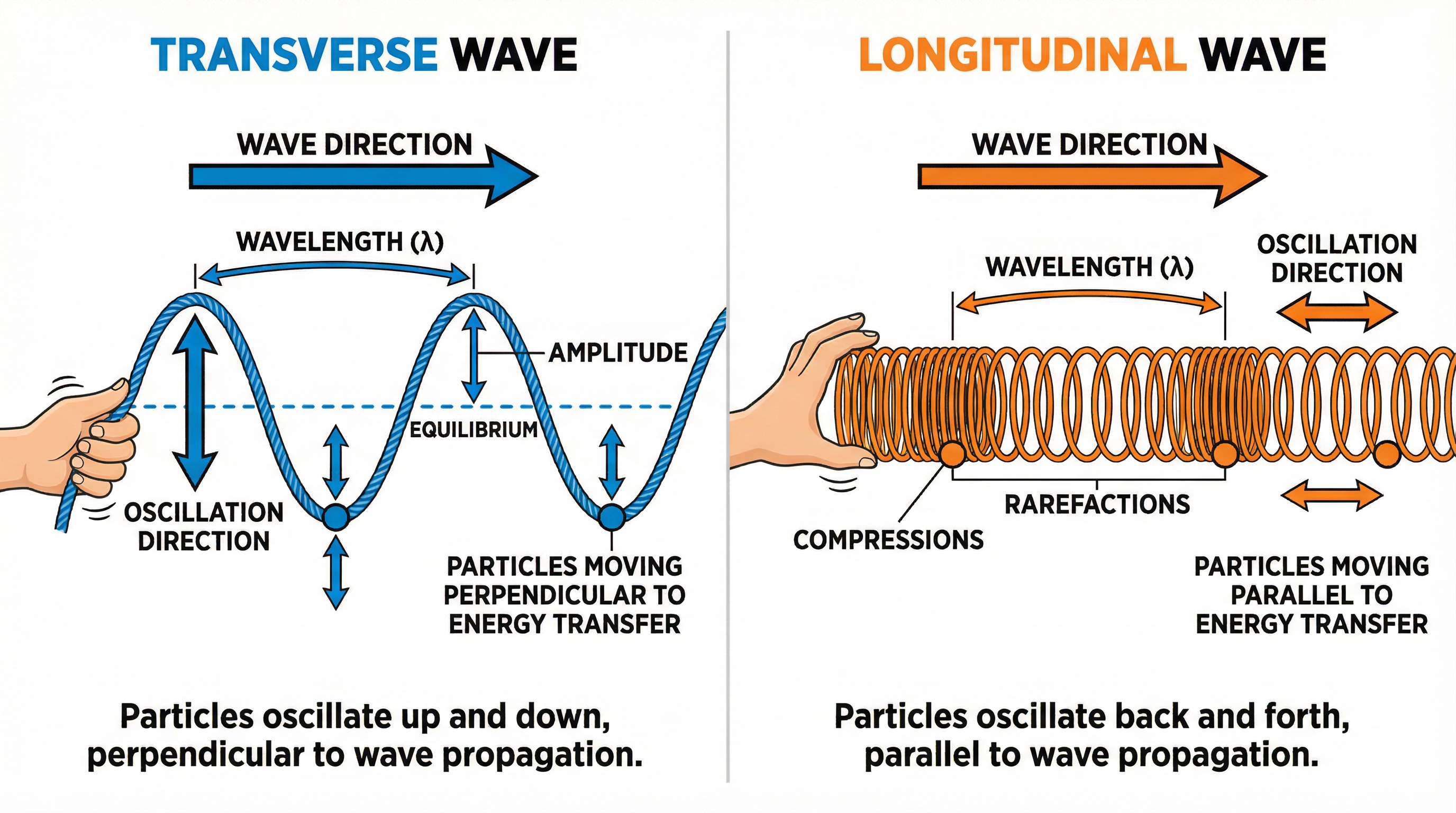
Waves are classified into two main types based on the direction of their oscillations relative to the direction of energy transfer. This is a core concept that you must be able to explain clearly.

Transverse Waves: In a transverse wave, the oscillations of the particles are perpendicular (at a 90-degree angle) to the direction of energy transfer. Imagine shaking a rope up and down: the wave travels along the rope, but the rope itself moves vertically. All electromagnetic waves, such as light and radio waves, are transverse. Water waves are another common example.

Longitudinal Waves: In a longitudinal wave, the oscillations of the particles are parallel to the direction of energy transfer. Sound waves are the primary example. As a sound wave travels through the air, it creates areas of compression (where particles are close together) and rarefaction (where particles are spread apart). The air particles vibrate back and forth in the same direction that the sound energy is travelling.

Concept 2: Wave Properties

To describe waves accurately, we use several key properties:

• Amplitude (A): The maximum displacement of a point on a wave from its undisturbed position. A larger amplitude corresponds to more energy being transferred.
• Wavelength (λ): The distance between two corresponding points on adjacent waves (e.g., from crest to crest or compression to compression). It is measured in metres (m).
• Frequency (f): The number of complete waves passing a certain point per second. It is measured in Hertz (Hz).
• Period (T): The time it takes for one complete wave to pass a point. It is the inverse of frequency (T = 1/f) and is measured in seconds (s).
• Wave Speed (v): The speed at which the energy is transferred through the medium. It is measured in metres per second (m/s).

Concept 3: The Wave Equation

The relationship between wave speed, frequency, and wavelength is described by the wave equation, which is provided on your formula sheet but is essential to master.

wave speed = frequency × wavelength

v = f × λThis equation is fundamental to solving many exam questions. You will often be given two of the values and asked to calculate the third. It is crucial to be comfortable rearranging the equation and to pay close attention to units, especially converting kHz and MHz to Hz.

Concept 4: The Electromagnetic Spectrum

The electromagnetic (EM) spectrum is a continuous range of transverse waves that travel at the speed of light in a vacuum (3.0 x 10⁸ m/s). They are grouped into seven main types based on their wavelength and frequency.

From longest wavelength to shortest wavelength (and lowest frequency to highest frequency), the order is:

Radio waves → Microwaves → Infrared → Visible light → Ultraviolet → X-rays → Gamma raysFor the exam, you need to know the order of the spectrum and the main uses and dangers of each type of wave.

Concept 5: Wave Interactions

Waves can interact with matter in several ways:

• Reflection: The wave bounces off a surface. The law of reflection states that the angle of incidence equals the angle of reflection.
• Refraction: The wave changes direction as it passes from one medium to another. This is caused by a change in the wave's speed. When light enters a denser medium, it slows down and bends towards the normal. When it enters a less dense medium, it speeds up and bends away from the normal.
• Absorption: The wave is absorbed by the material, and its energy is transferred to the material.
• Transmission: The wave passes through the material.

Mathematical/Scientific Relationships

• Wave Speed Equation: v = f × λ (Given on formula sheet)
  • v: wave speed (m/s)
  • f: frequency (Hz)
  • λ: wavelength (m)
• Period and Frequency: T = 1 / f (Must memorise)
  • T: period (s)
  • f: frequency (Hz)

Practical Applications

Core Practical: Measuring Wave Properties

This practical involves using a ripple tank to measure the frequency, wavelength, and speed of water waves.

• Apparatus: Ripple tank, lamp, power pack, wooden rod, stroboscope, ruler.
• Method:
  1. Set up the ripple tank with a shallow layer of water.
  2. Use the wooden rod to create waves of a constant frequency.
  3. Use the stroboscope to ‘freeze’ the wave pattern. The frequency of the stroboscope at which the waves appear stationary is equal to the frequency of the waves.
  4. Measure the wavelength by placing a ruler on the screen and measuring the distance between several consecutive wavefronts, then dividing by the number of gaps to find the average wavelength.
  5. Calculate the wave speed using v = f × λ.
• Common Errors: Parallax error when measuring wavelength; difficulty in accurately judging when the waves are ‘frozen’ by the stroboscope.

Graph/Data Skills

In the context of waves, you may be asked to interpret displacement-distance graphs and displacement-time graphs.

• Displacement-Distance Graph: Shows the displacement of all particles along the wave at a single moment in time. You can determine the wavelength and amplitude from this graph.
• Displacement-Time Graph: Shows the displacement of a single particle as the wave passes over time. You can determine the period and amplitude from this graph, and then calculate the frequency (f = 1/T).